题目内容

17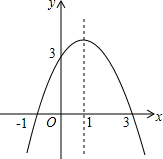．抛物线y=-x2+（m-1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求它与x轴的交点和抛物线顶点的坐标．

分析 （1）把点（0，3）坐标代入即可求出m的值；
（2）由（1）可知抛物线的解析式，进而可求出它与x轴的交点和抛物线顶点的坐标．

解答 解：（1）把（0，3）代入y=-x2+（m-1）x+m得，m=3，
故抛物线的解析式为y=-x2+2x+3；

（2）当y=0时，0=-x2+2x+3，
解得，x=1或x=3，
则抛物线与x轴的交点是（-1，0）、（3，0），
∵y=-x2+2x+3=-（x-1）2+4，
∴抛物线的顶点是（1，4）．

点评 此题考查了待定系数法求二次函数解析式，抛物线和x轴交点坐标，以及二次函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．

练习册系列答案
相关题目
7．乘雪橇沿倾斜角是30°的斜坡滑下，滑下的路程S（米）与时间t（秒）间的关系式为S=10t+t2，若滑到坡底的时间为2秒，则此人下滑的高度为（　　）
A．24米B．12米C．12$\sqrt{3}$米D．6米
8．一组数据2，3，3，4，4，3，5，5，它的众数是3．
5．二次函数y=ax2+1的图象一定经过的点是（　　）
A．（1，0）B．（-1，0）C．（0，1）D．（0，-1）
12．将△ABC绕点A旋转一定角度后与△ADE重合，如果△ABC的面积是12cm2，那么△ADE的面积是12cm2．
2．小明做了以下几道计算题：①-12014=1；②（-2$\frac{1}{3}$）2=-8$\frac{1}{27}$；③-22÷（-2）2=1；④-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$；⑤3$\frac{1}{4}$×$（-3.25）-6\frac{3}{4}×3.25$=-32.5；⑥-5+$\frac{1}{3}×\frac{3}{5}$=-25．请你帮他检查一下，他一共做对了（　　）
A．2道题B．3道题C．4道题D．5道题
9．在-5，-9，-3.5，-0.01，-2，-12各数中，最大的数是（　　）
A．-12B．-9C．-0.01D．-5
6．某电信局收取网费如下：163网费为每小时3元；169网费为每小时2元，但要收取15元月租费．设网费为y（元），上网时间为x（时）．分别写出y与x的函数关系式，某网民每月上网19小时，他应选那种上网方式．
7．问题提出；怎样计算1×2+2×3+3×4+…+（n-1）×n呢？
（1）材料学习；计算1+2+3…+n
因为1=$\frac{1}{2}$（1×2-0×1）；2=$\frac{1}{2}$（2×3-1×2）；3=$\frac{1}{2}$（3×4-2×3）
…，n=$\frac{1}{2}$[n（n+1）-（n-1）n]
所以1+2+3+…+n
=$\frac{1}{2}$（1×2-0×1）+$\frac{1}{2}$（2×3-1×2）+$\frac{1}{2}$（3×4-2×3）+…+$\frac{1}{2}$[n（n+1）-（n-1）n]
=$\frac{1}{2}$[1×2-0×1+2×3-1×2+3×4-2×3+…+n（n+1）-（n-1）n]=$\frac{1}{2}$n（n+1）
（2）探究应用
观察规律：①1×2=$\frac{1}{3}$（1×2×3-0×12）；②2×3=$\frac{1}{3}$（2×3×4-1×2×3）；
③3×4=$\frac{1}{3}$（3×4×5-2×3×4）；…
猜想归纳：
根据（2）中观察的规律直接写出：4×5=$\frac{1}{3}$（4×5×6-3×4×5）
（n-1）×n=$\frac{1}{3}$[（n-1）n（n+1）-（n-2）（n-1）n]
问题解决：
1×2+2×3+3×4+4×5…+（n-1）×n
=$\frac{1}{3}$（1×2×3-0×1×2）+$\frac{1}{3}$（2×3×4-1×2×3）+$\frac{1}{3}$（3×4×5-2×3×4）+…+$\frac{1}{3}$[（n-1）n（n+1）-（n-2）（n-1）n]
=$\frac{1}{3}$[1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+（n-1）n（n+1）-（n-2）（n-1）n]=$\frac{1}{3}$（n-1）n（n+1）
（3）拓展延伸
根据（1）、（2）中的规律，请直接写出1×2×3+2×3×4+3×4×5+…+（n-2）（n-1）n=$\frac{1}{4}$（n-2）（n-1）n（n+1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网