题目内容
5.二次函数y=ax2+1的图象一定经过的点是( )| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
分析 把A、B、C、D分别代入y=ax2+1即可判断.
解答 解:∵x=0时,y=1,
x=±1时,y=a+1,
∴二次函数y=ax2+1的图象必过点(0,1).
故选C.
点评 本题考查了二次函数图象上点的坐标特征:图象上的点的坐标代入解析式成立.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.下列各对数中,互为相反数的一对数是( )
| A. | -23与-32 | B. | (-2)3与-23 | C. | (-3)2与-32 | D. | -(-1)与1 |
13.能与4cm,9cm长的两根木棒首尾相接,钉成一个三角形的木棒是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
10.关于旋转的性质,以下说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | |
| B. | 对应点与旋转中心所连线线段的夹角等于旋转角 | |
| C. | 旋转前、后的图形全等 | |
| D. | 对应点的连线必经过旋转中心且被旋转中心平分 |
14.已知0.8622=0.7396,若x2=0.7396,则x的值等于( )
| A. | 0.862 | B. | -0.862 | C. | ±0.862 | D. | ±8.62 |
15.以下列各组数为边长,能构成直角三角形的是( )
| A. | 12,15,20 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 0.3,0.4,0.5 | D. | 32,42,52 |
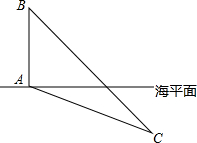 在某次军事演习中,军舰A测得潜艇C的俯角为30°,位于军舰A正上方800m的直升机B测得潜艇C的俯角为45°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留准确值)
在某次军事演习中,军舰A测得潜艇C的俯角为30°,位于军舰A正上方800m的直升机B测得潜艇C的俯角为45°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留准确值)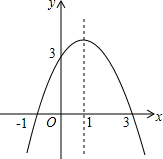 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).