题目内容
12.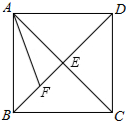 已知:如图,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F,求证:EF+AE=AB.
已知:如图,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F,求证:EF+AE=AB.
分析 由正方形对角线的性质可得:AE⊥BE,∠ABE=45°,过点F作FH⊥AB于点H,可得△BFH是等腰直角三角形,进而可得FH=BH,然后由角平分线的性质,可得EF=HF=BH,然后根据HL定理可证Rt△AHF≌Rt△AEF,进而可得AE=AH,从而可得EF+AE=BH+AH=AB.
解答 证明:过点F作FH⊥AB于点H,
在正方形ABCD中,
∵对角线AC与BD相交于点E,
∴AE⊥BE,∠ABE=45°,
∵FH⊥AB,
∴∠BFH=45°,
∴∠ABE=∠BFH,
∴BH=FH,
∵AF平分∠BAC,且FH⊥AB,AE⊥BE,
∴EF=HF=BH,
在Rt△AHF和Rt△AEF中,
$\left\{\begin{array}{l}{HF=EF}\\{AF=AF}\end{array}\right.$,
∴Rt△AHF≌Rt△AEF(HL),
∴AE=AH,
∴EF+AE=BH+AH=AB,
即EF+AE=AB.
点评 此题考查了正方形的性质及全等三角形的判定与性质,解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,发挥它们的作用构造全等三角形,然后利用全等三角形的性质解题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )| A. | △ADE≌△ADC | B. | DE=DC | C. | ∠ADE=∠ADC | D. | BD=DC |
4.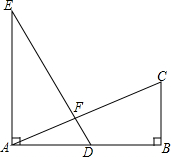 如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )
如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )
①DE=AC;②DE⊥AC;③∠EAF=∠ADF;④∠C=∠ADF;⑤∠C=∠E.
 如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )
如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列式中成立的有( )①DE=AC;②DE⊥AC;③∠EAF=∠ADF;④∠C=∠ADF;⑤∠C=∠E.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.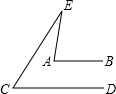 如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
 如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )
如图所示,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )| A. | 28° | B. | 52° | C. | 80° | D. | 70° |
 已知P为平行四边形ABCD的BC延长线上一点,AP交CD于Q,如果△DPQ的面积是100cm2,求△BCQ的面积.
已知P为平行四边形ABCD的BC延长线上一点,AP交CD于Q,如果△DPQ的面积是100cm2,求△BCQ的面积.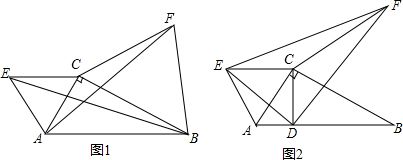
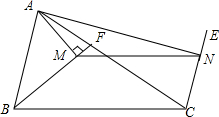 如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,
如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,
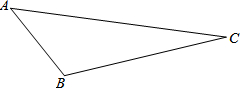 已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要
已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要