题目内容
3．
已知P为平行四边形ABCD的BC延长线上一点，AP交CD于Q，如果△DPQ的面积是100cm2，求△BCQ的面积．
分析 由四边形ABCD是平行四边形，易证得△ADQ∽△PCQ，然后由相似三角形的对应边成比例，证得DQ：CQ=AQ：PQ，又由等高三角形面积的比等于其对应底的比，可得S△ADQ：S△DPQ=AQ：PQ，S△ADQ：S△BCQ=DQ：CQ，继而求得答案．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△ADQ∽△PCQ，
∴DQ：CQ=AQ：PQ，
∵S△ADQ：S△DPQ=AQ：PQ，S△ADQ：S△BCQ=DQ：CQ，
∴S△BCQ=S△DPQ=100cm2．
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．注意等高三角形面积的比等于对应底的比．
练习册系列答案
相关题目
14．
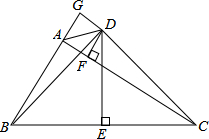如图，在△ABC中，AC＞AB，DE（点D在△ABC的外部）垂直平分BC，交BC于点E，连接BD，CD，AD，过点D作DF⊥AC于点F，延长BA到点G，使得BG=CF，连接DG，若∠DBC-∠GBD=∠BCA，则下列说法中不正确的是（ ）
如图，在△ABC中，AC＞AB，DE（点D在△ABC的外部）垂直平分BC，交BC于点E，连接BD，CD，AD，过点D作DF⊥AC于点F，延长BA到点G，使得BG=CF，连接DG，若∠DBC-∠GBD=∠BCA，则下列说法中不正确的是（ ）| A． | ∠BGD=90° | B． | AD平分∠GAC | C． | ∠GDB=∠FDC | D． | ∠BDG=90° |
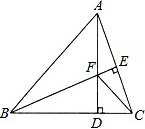△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC，∠BAD=45°，AD与BE交于点F，连接CF，
甲乙两人住的房间号都是三位数的完全平方数，当他们将自己的房间号写下来并排成形状时，他们惊呆了，这个数阵中每列（自上而下）两数组成的两位数也是完全平方数．请说说：他们各自房间号码是多少？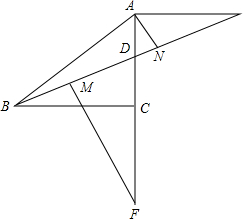
已知：如图，等腰Rt△ABC中，D为AC上一点，AE∥BC交BD延长线于E，AN⊥BE于N，在BE上截取MB=AN，过M作MF⊥BE交AC延长线于F，求证：CF=BC．
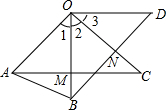已知，OA=OB，OC=OD，∠1=∠2=∠3，AC交OB于M，BD交OC于N，求证：OM=ON．
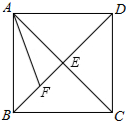已知：如图，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F，求证：EF+AE=AB．
13．在二元一次方程x+3y=1的解中，当x=4时，对应的y的值是（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | -1 | D． | 4 |