题目内容
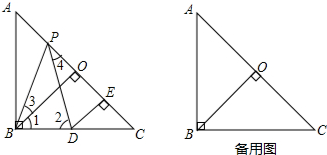
7.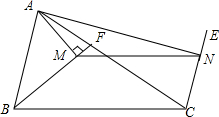 如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,
如图,BF是△ABC的角平分线,AM⊥BF于M,CE平分△ABC的外角,AN⊥CE于N,(1)求证:MN∥BC;
(2)若AB=c,AC=b,BC=a,求MN的长.
分析 (1)延长AM交BC于G,延长AN交BC的延长线于点H,先根据AAS证明△ABM≌△GBM,得出AM=GM,同理得出AN=HN,证出MN是△AGH的中位线,即可得出MN∥GH,MN=$\frac{1}{2}$GH;
(2)由△ABM≌△GBM得出BG=AB=c,同理得:CH=AC=b,求出GH=a-c+b,根据中位线定理即可求出MN.
解答 解:(1)延长AM交BC于G,延长AN交BC的延长线于点H,如图所示: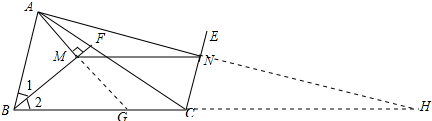 ∵BF是△ABC的角平分线,AM⊥BF于M,
∵BF是△ABC的角平分线,AM⊥BF于M,
∴∠1=∠2,∠AMB=∠GMB=90°,
在△ABM和△GBM中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{BM=BM}&{\;}\\{∠AMB=∠GMB}&{\;}\end{array}\right.$,
∴△ABM≌△GBM(ASA),
∴AM=GM,
同理可证:AN=HN,
∴MN是△AGH的中位线,
∴MN∥GH,MN=$\frac{1}{2}$GH,
∴MN∥BC;
(2)由△ABM≌△GBM得:BG=AB=c,
同理得:CH=AC=b,
∴GC=BC-BG=a-c,
∴GH=a-c+b,
∴MN=$\frac{1}{2}$(a-c+b).
点评 本题考查了全等三角形的判定与性质以及三角形中位线定理;通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.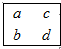 如图是2012年11月份的日历,现用一长方形在日历中任意框出4个数,请用一个等式表示a,b,c,d之间的关系,下列表示正确的是( )
如图是2012年11月份的日历,现用一长方形在日历中任意框出4个数,请用一个等式表示a,b,c,d之间的关系,下列表示正确的是( )
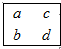 如图是2012年11月份的日历,现用一长方形在日历中任意框出4个数,请用一个等式表示a,b,c,d之间的关系,下列表示正确的是( )
如图是2012年11月份的日历,现用一长方形在日历中任意框出4个数,请用一个等式表示a,b,c,d之间的关系,下列表示正确的是( )| A. | a+d=b+c | B. | a+c=b+d | C. | a+b=c+d | D. | a+d+1=b+c |
 甲乙两人住的房间号都是三位数的完全平方数,当他们将自己的房间号写下来并排成形状时,他们惊呆了,这个数阵中每列(自上而下)两数组成的两位数也是完全平方数.请说说:他们各自房间号码是多少?
甲乙两人住的房间号都是三位数的完全平方数,当他们将自己的房间号写下来并排成形状时,他们惊呆了,这个数阵中每列(自上而下)两数组成的两位数也是完全平方数.请说说:他们各自房间号码是多少?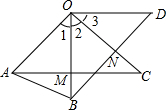 已知,OA=OB,OC=OD,∠1=∠2=∠3,AC交OB于M,BD交OC于N,求证:OM=ON.
已知,OA=OB,OC=OD,∠1=∠2=∠3,AC交OB于M,BD交OC于N,求证:OM=ON. B、C、D三点共线,且有正△ABC与正△CDE,F为AD的中点,G为BE中点,求证:CF=FG=CG.
B、C、D三点共线,且有正△ABC与正△CDE,F为AD的中点,G为BE中点,求证:CF=FG=CG.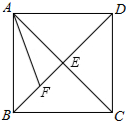 已知:如图,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F,求证:EF+AE=AB.
已知:如图,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F,求证:EF+AE=AB.