题目内容
 如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),
如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),(1)用直尺和圆规在边CD上找一个点P,使△ADP沿着直线AP翻折后D点正好落在BC边上的Q点(不写作法,保留作图痕迹).连结AP,AQ,PQ
(2)在(1)中作的新图形中,已知AB=5,AD=13,求CP的长.
(3)在(2)的条件下,点M为直线BC上一动点,△PQM为等腰三角形,请直接写出BM的长.
考点:作图—复杂作图,等腰三角形的判定,矩形的性质
专题:
分析:(1)以A为圆心,以AD为半径交BC于点Q,作出∠DAQ的平分线,交CD于点P;
(2)利用△ABQ∽△QCP,根据相似三角形的对应边的比相等求得CP的值;
(3)求得PQ的长,然后利用等腰三角形的定义即可进行讨论求解.
(2)利用△ABQ∽△QCP,根据相似三角形的对应边的比相等求得CP的值;
(3)求得PQ的长,然后利用等腰三角形的定义即可进行讨论求解.
解答: 解:(1)点P就是所求的图形;
解:(1)点P就是所求的图形;
(2)在直角△ABQ中,BQ=
=
=12,
则QC=BC-BQ=13-12=1,
∵∠AQP=∠ADC=90°,
∴∠AQB+∠PQC=90°,
又∵直角△ABQ中,∠BAQ+∠AQP=90°,
∴∠PQC=∠BAQ,
又∵∠B=∠C=90°,
∴△ABQ∽△QCP,
∴
=
,即
=
,
解得:CP=
;
(3)当P是顶角顶点时,M在CQ的延长线上,CM=CQ=1,
则BM=13+1=14;
在直角△PCQ中,PQ=
=
=
,
当Q是等腰三角形的顶角顶点时,QM=PQ=
,当M在BQ上时,BM=BQ-QM=12-
=
;
当Q在BQ的延长线上时,BM=BQ+QM=12+
=
;
当M是等腰三角形的顶角顶点时,M在PQ的中垂线上,如图.
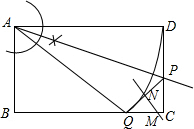 PN=
PN=
PQ=
×
=
,
∵∠PQC=∠BAQ,∠B=∠QNM=90°,
∴△ABQ∽△QNM,
∴
=
,即
=
,
解得:QM=
,
则BM=BQ+QM=12+
=
.
总之,BM=14或
或
或
.
 解:(1)点P就是所求的图形;
解:(1)点P就是所求的图形;(2)在直角△ABQ中,BQ=
| AQ2-AB2 |
| 132-52 |
则QC=BC-BQ=13-12=1,
∵∠AQP=∠ADC=90°,
∴∠AQB+∠PQC=90°,
又∵直角△ABQ中,∠BAQ+∠AQP=90°,
∴∠PQC=∠BAQ,
又∵∠B=∠C=90°,
∴△ABQ∽△QCP,
∴
| CP |
| BQ |
| QC |
| AB |
| CP |
| 12 |
| 1 |
| 5 |
解得:CP=
| 12 |
| 5 |
(3)当P是顶角顶点时,M在CQ的延长线上,CM=CQ=1,
则BM=13+1=14;
在直角△PCQ中,PQ=
| PC2+CQ2 |
(
|
| 13 |
| 5 |
当Q是等腰三角形的顶角顶点时,QM=PQ=
| 13 |
| 5 |
| 13 |
| 5 |
| 47 |
| 5 |
当Q在BQ的延长线上时,BM=BQ+QM=12+
| 13 |
| 5 |
| 73 |
| 5 |
当M是等腰三角形的顶角顶点时,M在PQ的中垂线上,如图.
 PN=
PN=| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 5 |
| 13 |
| 10 |
∵∠PQC=∠BAQ,∠B=∠QNM=90°,
∴△ABQ∽△QNM,
∴
| QM |
| AQ |
| QN |
| AB |
| QM |
| 13 |
| ||
| 5 |
解得:QM=
| 169 |
| 50 |
则BM=BQ+QM=12+
| 169 |
| 50 |
| 769 |
| 50 |
总之,BM=14或
| 47 |
| 5 |
| 73 |
| 5 |
| 769 |
| 50 |
点评:本题考查了矩形的性质以及相似三角形的判定与性质,正确对等腰三角形进行讨论是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
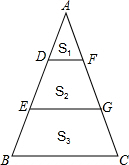 如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )
如图,D、E是AB的三等分点,且DF∥EG∥BC,则图中三部分图形的面积比S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:3:6 |
 如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0).
如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0). 如图,点C为线段AB上的一点,AC=
如图,点C为线段AB上的一点,AC=
 已知:如图,AD=BC,AC=BD.
已知:如图,AD=BC,AC=BD.