题目内容
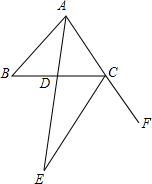 如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为
如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义可得∠EAC=
∠BAC,∠ECF=
∠BCF,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BCF=∠ABC+∠BAC,∠ECF=∠AEC+∠EAC,然后整理即可得到∠AEC=
∠ABC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AE、CE分别是∠BAC和∠BCF的平分线,
∴∠EAC=
∠BAC,∠ECF=
∠BCF,
由三角形的外角性质得,∠BCF=∠ABC+∠BAC,∠ECF=∠AEC+∠EAC,
∴∠AEC+∠EAC=
(∠ABC+∠BAC),
∴∠AEC=
∠ABC,
∵∠ABC=31°,
∴∠AEC=
×31=15.5°.
故答案为:15.5°.
∴∠EAC=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠BCF=∠ABC+∠BAC,∠ECF=∠AEC+∠EAC,
∴∠AEC+∠EAC=
| 1 |
| 2 |
∴∠AEC=
| 1 |
| 2 |
∵∠ABC=31°,
∴∠AEC=
| 1 |
| 2 |
故答案为:15.5°.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质与定理并求出∠AEC=
∠ABC是解题的关键.
| 1 |
| 2 |

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
用长4米的铝材制成一个矩形窗框,使它的面积为0.75米2.若设它的一边长为x米,根据题意列出关于x的方程为( )
| A、x(2-x)=0.75 |
| B、2x(2-x)=0.75 |
| C、x(4-2x)=0.75 |
| D、x(4-x)=0.75 |
如果-5a是正数,那么( )
| A、a>0 | B、a<0 |
| C、a≥0 | D、a≤0 |
 如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为
如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为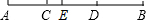 如图,点C为线段AB上的一点,AC=
如图,点C为线段AB上的一点,AC=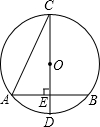 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2