题目内容
 如图,已知OA1=A1A2=A2A3=A3A4=…=AnAn+1=1,∠OA1A2=∠OA2A3=…=
如图,已知OA1=A1A2=A2A3=A3A4=…=AnAn+1=1,∠OA1A2=∠OA2A3=…=∠OAnAn+1=90°,各三角形的面积分别为S1,S2,S3,…,Sn,分析下列各式,然后回答问题:
(
| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
(1)试用含n的等式(n为正整数)表示上述变化规律;
(2)推测OA10的值;
(3)求S12+S22+S32+…+S102的值.
考点:二次根式的化简求值
专题:规律型
分析:(1)观察各等式和勾股定理、三角形面积公式易得(
)2+1=n+1,Sn=
;
(2)利用勾股定理可得到OA10=
;
(3)利用二次根式的性质进行计算.
| n |
| ||
| 2 |
(2)利用勾股定理可得到OA10=
| 10 |
(3)利用二次根式的性质进行计算.
解答:解:(1)(
)2+1=n+1,Sn=
;
(2)OA10=
;
(3)S12+S22+S32+…+S102=(
)2+(
)2+(
)2+…+(
)2=
(1+2+3+…+10)=
.
| n |
| ||
| 2 |
(2)OA10=
| 10 |
(3)S12+S22+S32+…+S102=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 55 |
| 4 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
已知PA,PB是⊙O的两条切线,点A,B为切点,且∠APB=50°.过点A作⊙O的直径AC,连结BC,则∠PBC等于( )
| A、165° | B、160° |
| C、155° | D、150° |
多项式-4a2b2+12a2b3-8a3b2c的公因式是( )
| A、-4a2b2c |
| B、-a2b2 |
| C、-4a3b2c |
| D、-4a2b2 |
 如图,过?ABCD的顶点D,C分别向对边AB所在直线作垂线DE和CF,垂足分别为点E,F,求证:AE=BF.
如图,过?ABCD的顶点D,C分别向对边AB所在直线作垂线DE和CF,垂足分别为点E,F,求证:AE=BF.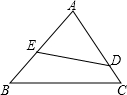 如图,D,E分别是AC,AB上的点,
如图,D,E分别是AC,AB上的点, 如图,在正方形ABCD中,E为AD的中点,F是BA延长线上一点,AF=
如图,在正方形ABCD中,E为AD的中点,F是BA延长线上一点,AF= 如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图.
如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图.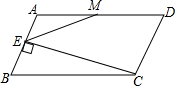 如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.
如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.