题目内容
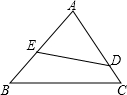如图，D，E分别是AC，AB上的点，| AE |
| AC |
| AD |
| AB |
| 2 |
| 3 |
考点：相似三角形的判定与性质
专题：
分析：根据相似三角形的判定证△ADE∽△ABC，根据相似三角形的性质求出△ADE的面积，相减即可求出答案．
解答：解：∵
=
=
，∠A=∠A，
∴△ADE∽△ABC，
∴
=
，
∵△ABC的面积为60cm2，
∴△ADE的面积是
×60cm2=
cm2，
∴四边形BCDE的面积是60cm2-
cm2=
cm2，
答：四边形BCDE的面积是
cm2．
| AE |
| AC |
| AD |
| AB |
| 2 |
| 3 |
∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| 4 |
| 9 |
∵△ABC的面积为60cm2，
∴△ADE的面积是
| 4 |
| 9 |
| 80 |
| 3 |
∴四边形BCDE的面积是60cm2-
| 80 |
| 3 |
| 100 |
| 3 |
答：四边形BCDE的面积是
| 100 |
| 3 |
点评：本题主要考查对相似三角形的性质和判定的理解和掌握，能熟练地运用性质进行推理是解此题的关键．
练习册系列答案
相关题目
若多项式（x+2y）2-6x（x+2y）有一个因式为x+2y，则另一个因式为（ ）
| A、2x-5y |
| B、-5x-2y |
| C、-5x+2y |
| D、5x+2y |
下列各式中，正确的是（ ）
A、已知ab＞0，则
| ||||||||||||||||
B、2
| ||||||||||||||||
C、
| ||||||||||||||||
D、
|
如图，已知OA1=A1A2=A2A3=A3A4=…=AnAn+1=1，∠OA1A2=∠OA2A3=…=
如图所示是一个由若干个小立方体叠成的几何体的俯视图，每个小方格中的数字表示该位置上重叠的小立方体的个数，请你画出它的主视图和左视图．
