题目内容
8.已知二次函数y=ax2+bx+c的图象与反比例函数y=$\frac{a+3}{x}$的图象交于点A(a,-2).(1)求a的值;
(2)设这个二次函数的图象与y轴交于点B,且∠ABO=135°,求这个二次函数的图象的顶点的坐标.
分析 (1)根据反比例函数图象上点的特征,把点A的坐标代入反比例函数解析式计算即可;
(2)作AC⊥x轴于C,根据∠ABO=135°,得到△ABC为等腰直角三角形,求出点B的坐标,求出二次函数解析式,根据二次函数的性质求出顶点坐标.
解答 解:(1)∵反比例函数y=$\frac{a+3}{x}$的图象经过点A(a,-2),
∴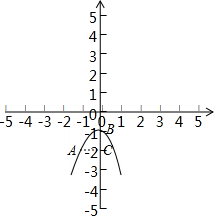 a+3=-2a,
a+3=-2a,
解得,a=-1;
(2)作AC⊥x轴于C,
由(1)得,点A的坐标为(-1,-2),
∴AC=1,OC=2,
∵∠ABO=135°,
∴∠ABC=45°,
∴BC=AC=1,
∴OB=1,
则点B的坐标为(0,-1),
∴c=-1,
∵y=ax2+bx+c的图象经过点A(-1,-2),
∴b=0,
∴二次函数的解析式为y=-x2-1,
∴这个二次函数的图象的顶点的坐标为(0,-1).
点评 本题考查的是二次函数的图象和性质、反比例函数的图象和性质以及待定系数法求函数解析式,掌握函数的性质、灵活运用数形结合思想是解题的关键.

练习册系列答案
相关题目
18.已知点E在如图1的长方形纸带AD上,作∠DEF=α,将纸带沿EF折叠成图2,再沿BF折叠成图3中的∠CFE=114°,那么α的大小为( )
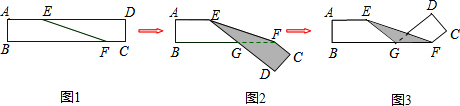

| A. | 27° | B. | 26° | C. | 23° | D. | 22° |
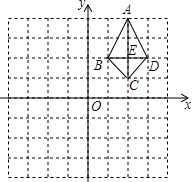 如图,四边形ABCD的对角线AC、BD相交于点E.
如图,四边形ABCD的对角线AC、BD相交于点E.