题目内容
2.平行四边形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,则平行四边形ABCD的面积为15$\sqrt{3}$.分析 过点A作AE⊥BD于E,设OE=a,则AE=$\sqrt{3}$a,OA=2a,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,△ABD的面积可求出,由平行四边形的性质可知:?ABCD的面积=2S△ABD,问题得解.
解答 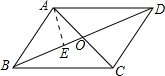 解:过点A作AE⊥BD于E,
解:过点A作AE⊥BD于E,
∵四边形ABCD是平行四边形,
∴OD=$\frac{1}{2}$BD=$\frac{1}{2}$×10=5,
∵∠BOC=120°,
∴∠AOE=60°,
设OE=a,则AE=$\sqrt{3}$a,OA=2a,
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴(5+a)2+($\sqrt{3}$a)2=72,
解得:a=$\frac{3}{2}$,
∴AE=$\sqrt{3}$×$\frac{3}{2}$=$\frac{3\sqrt{3}}{2}$,
∴?ABCD的面积=2S△ABD=2×10×$\frac{3\sqrt{3}}{2}$×$\frac{1}{2}$=15$\sqrt{3}$.
故答案为:15$\sqrt{3}$.
点评 此题考查了平行四边形的性质以及勾股定理,注意掌握数形结合思想与方程思想的应用,利用勾股定理得出a的值是解题关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | -$\sqrt{0.64}$=0.8 | C. | ±$\sqrt{0.81}$=±0.9 | D. | -$\sqrt{49}$=±7 |
7.△ABC的三边之比为3:4:5,与其相似的△DEF的最短边是9cm,则其最长边的长是( )
| A. | 5cm | B. | 10cm | C. | 15cm | D. | 30cm |
11.若分$\frac{x+y}{2xy}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的$\frac{1}{3}$ | D. | 是原来的一半 |

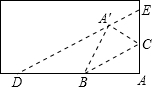 小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )
小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )