题目内容
14.某校八年级的体育老师为了了解本年级学生喜欢球类运动的情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如下两幅不完整的统计图(说明:每位学生只选一种自己最喜欢的一种球类),请你根据这两幅图形解答下列问题:(1)在本次调查中,体育老师一共调查了200名学生;
(2)将两个不完整的统计图补充完整;
(3)八(一)班在本次调查中有3名女生和2名男生喜欢篮球,现从这5名学生中任意抽取2名学生当篮球队的队长,请用列表或画树状图的方法求出刚好抽到一男一女的概率.

分析 (1)读图可知喜欢足球的有40人,占20%,求出总人数;
(2)根据总人数求出喜欢乒乓球的人数所占的百分比,得出喜欢排球的人数,再根据喜欢篮球的人数所占的百分比求出喜欢篮球的人数,从而补全统计图;
(3)用列表法求出总的事件所发生的数目,再根据概率公式即可求出刚好抽到一男一女的概率.
解答 解:(1)∵喜欢足球的有40人,占20%,
∴一共调查了:40÷20%=200(人),
故答案为:200;
(2)∵喜欢乒乓球人数为60人,
∴所占百分比为:$\frac{60}{200}$×100%=30%,
∴喜欢排球的人数所占的百分比是1-20%-30%-40%=10%
∴喜欢排球的人数为:200×10%=20(人),
∴喜欢篮球的人数为200×40%=80(人),
由以上信息补全条形统计图得: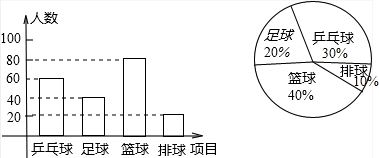
(3)列表或画树状图如下:
| 女1 | 女2 | 女3 | 男1 | 男2 | |
| 女1 | (女2,女1) | (女3,女1) | (男1,女1) | (男2,女1) | |
| 女2 | (女1,女2) | (女3,女2) | (男1,女2) | (男2,女2) | |
| 女3 | (女1,女3) | (女2,女3) | (男1,女3) | (男2,女3) | |
| 男1 | (女1,男1) | (女2,男1) | (女3,男1) | (男1,男1) | |
| 男2 | (女1,男2) | (女2,男2) | (女3,男2) | (男1,男2) |
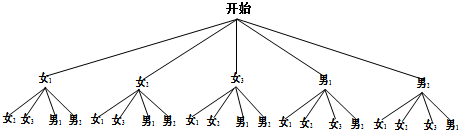
∵共有20种等可能的结果,恰为一男一女的有12种,
∴抽到一男一女的概率为P(一男一女)=$\frac{12}{20}$=$\frac{3}{5}$.
点评 本题考查学生的读图能力和求随机事件的概率,解题的关键是必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,难度适中.

练习册系列答案
相关题目
19.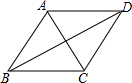 如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
 如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )| A. | △ABD与△ABC的周长相等 | |
| B. | 菱形的周长等于两条对角线长之和的两倍 | |
| C. | △ABD与△ADC的周长相等 | |
| D. | 菱形的面积等于两条对角线长之积的两分之一 |
6.关于x的方程mx-m=-x-1有解,则m的值是( )
| A. | m≠0 | B. | m≠1 | C. | m≠-1 | D. | m≠±1 |
3.如果a=(-99)0,b=(-0.1)-1,c=(-$\frac{5}{3}$)-2,那a,b,c三数的大小为( )
| A. | a>b>c | B. | c>a>b | C. | c<b<a | D. | a>c>b |
4.下列各式计算正确的是( )
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 5$\sqrt{3}$-2$\sqrt{2}$=3$\sqrt{3}$ | D. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
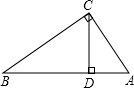 如图,已知AC⊥BC,CD⊥AB,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是8.
如图,已知AC⊥BC,CD⊥AB,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是8.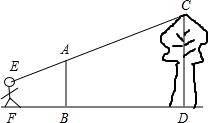 如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.