题目内容
5.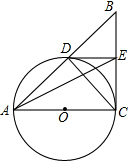 以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点.
以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点.(1)求证:DE是⊙O的切线;
(2)如果AD=4,BD=$\frac{9}{4}$,求DE的长;
(3)证明$\frac{{S}_{△BDC}}{{S}_{△BCA}}$=cos2B.
分析 (1)连结OD,由AC是⊙O的直径知∠ADC=∠CDB=90°,根据BE=EC知∠EDB=∠B,进而有∠ODA+∠EDB=∠A+∠B=90°,即∠ODE=90°,得证;
(2)由切割线定理知BC2=BD•BA,可求得BC长,根据DE=$\frac{1}{2}$BC可得;
(3)显然△BDC∽△BCA,可得$\frac{{S}_{△BDC}}{{S}_{△BCA}}$=$\frac{BD•DC}{AC•BC}$,根据cos2B=($\frac{BD}{BC}$)2可证得.
解答 (1)证明:连结OD,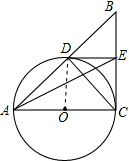
∵OA=OD,
∴∠ODA=∠A
∵AC是⊙O的直径,
∴∠ADC=∠CDB=90°,
∵BE=EC,
∴DE=$\frac{1}{2}$BC,即DE=BE,
∴∠EDB=∠B,
∴∠ODA+∠EDB=∠A+∠B=90°,
∴∠ODE=90°,OD为⊙O的半径,
∴DE是⊙O的切线;
(2)解:∵BC2=BD•BA,
∴BC2=$\frac{9}{4}$($\frac{9}{4}$+4),
解得BC=$\frac{15}{4}$,
则DE=$\frac{1}{2}$BC=$\frac{15}{8}$;
(3)证明:∵CD是Rt△ABC的斜边上的高,
∴△BDC∽△BCA,
∴$\frac{{S}_{△BDC}}{{S}_{△BCA}}$=$\frac{BD•DC}{AC•BC}$,
又∵cos2B=($\frac{BD}{BC}$)2,
∴$\frac{{S}_{△BDC}}{{S}_{△BCA}}$=cos2B.
点评 本题主要考查切线的判定与相似三角形的判定与性质及切割线定理的运用,连圆心与切点证垂直是证明切线的常用作法,证相切是本题的关键.

练习册系列答案
相关题目
6.下列各式不是多项式x3-x的因式的是( )
| A. | x | B. | 3x-1 | C. | x-1 | D. | x+1 |
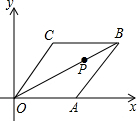 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).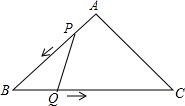 已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:
已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题: