题目内容
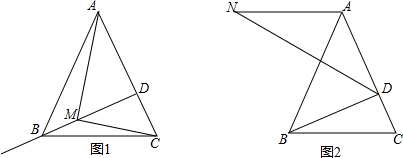
17.如图1,在△ABC中,AB=AC,BD⊥AC,垂足为D,且AD=4,DC=2,动点M以每秒2个单位长度的速度从点D出发,沿射线DB做匀速运动,设运动时间为t秒.(1)当t=1秒时,则CM=2$\sqrt{2}$;
(2)当t为何值时,∠AMC=90°;
(3)如图2,过点A作AN∥BC,并使得∠NDB=∠C,求AN•BC的值.
分析 (1)当t=1秒时,DM=2,由勾股定理求出CM即可;
(2)当∠AMC=90°时,由射影定理得出DM2=AD•DC,求出DM,即可得出结果;
(3)连接BN,由等腰三角形的性质、平行线的性质和已知条件得出∠BAN=∠NDB,证出A、D、B、N四点共圆,由圆周角定理得出AB是圆的直径,∠BNA=90°=∠CDB,证出△ABN∽△CBD,得出对应边成比例,即可得出结果.
解答 解:(1)当t=1秒时,DM=2,
∵BD⊥AC,
∴∠ADB=∠CDB=90°,
∴CM=$\sqrt{D{M}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故答案为:2$\sqrt{2}$;
(2)当∠AMC=90°时,
∵∠ADB=∠CDB=90°,
∴由射影定理得:DM2=AD•DC=4×2=8,
解得:DM=$\sqrt{8}$=2$\sqrt{2}$,
∴t=2$\sqrt{2}$÷2=$\sqrt{2}$(秒),
∴当t为$\sqrt{2}$秒时,∠AMC=90°;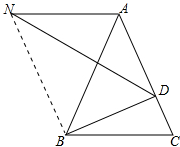
(3)连接BN,如图所示:
∵AB=AC=AD+DC=6,
∴∠ABC=∠C,
∵AN∥BC,
∴∠BAN=∠ABC,
∵∠NDB=∠C,
∴∠BAN=∠NDB,
∴A、D、B、N四点共圆,
∵∠ADB=90°,
∴AB是圆的直径,
∴∠BNA=90°=∠CDB,
又∵∠BAN=∠C,
∴△ABN∽△CBD,
∴$\frac{AN}{CD}=\frac{AB}{BC}$,
∴AN•BC=AB•CD=6×2=12.
点评 本题是相似形综合题目,考查了勾股定理、射影定理、相似三角形的判定与性质、四点共圆、圆周角定理等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线证明四点共圆,运用三角形相似采纳得出结果.

| A. | 每个小长方形的面积等于频数 | B. | 每个小长方形的面积等于频率 | ||
| C. | 频率=$\frac{频数}{数据总数}$ | D. | 各个小长方形面积和等于1 |
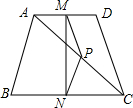 如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.
如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.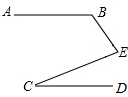 如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°.
如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°.