题目内容
7.图①、②分别是一把水平放置的椅子的效果图与椅子侧面的示意图,椅子高为AC,椅面宽BE为60cm,椅脚高ED为35cm,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点E的俯角为53°,求椅子高AC(精确到0.1cm).【参考数据:sin53°=0.739,cos53°=0.673,tan53°=1.099】
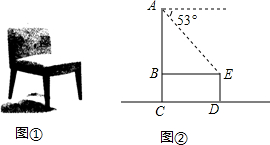
分析 要求AC的长,只要求出AB和BC的长即可,根据题意可知BC与DE的长相等,根据∠AEB=53°和BE的长可以求得AB的长,从而可以求得AC的长,本题得以解决.
解答 解:∵AC⊥BE,AC⊥CD,AC∥ED,
∴四边形BCDE是矩形,∠AEB=53°,
∴BC=DE=35,
在Rt△ABE中,∠ABE=90°,tan∠AEB=$\frac{AB}{BE}$,BE=60,
∴AB=BE•tan∠AEB=60×tan53°=60×1.009=65.94,
∴AC=AB+BC=65.94+35=100.94≈100.9cm,
即椅子的高约为100.9cm.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
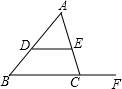 如图,DE∥BC,CF为BC的延长线,若∠ADE=50°,∠ACF=110°,则∠A=60°.
如图,DE∥BC,CF为BC的延长线,若∠ADE=50°,∠ACF=110°,则∠A=60°.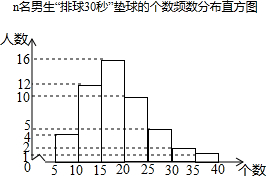 某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题: