题目内容
4.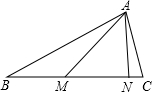 如图,△ABC中,AB=BC,M、N为BC边上的两点,且∠BAM=∠CAN,MN=AN.求∠MAC的度数.
如图,△ABC中,AB=BC,M、N为BC边上的两点,且∠BAM=∠CAN,MN=AN.求∠MAC的度数.
分析 设∠CAN=x,∠MAN=y,先表示出∠C为2x+y,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠ANM,再根据等边对等角的性质求出∠AMN=∠MAN,然后利用三角形的内角和定理列式求出x+y的度数,也就是∠MAC的度数.
解答 解:设∠CAN=x,∠MAN=y,
∵AB=BC,∠BAM=∠CAN,
∴∠C=∠BAC=2x+y,
∴∠ANM=x+(2x+y)=3x+y,
∵MN=AN,
∴∠AMN=∠MAN,
在△AMN中,2y+(3x+y)=180°,
解得x+y=60°,
即∠MAC=60°.
点评 本题主要考查了等腰三角形的性质和三角形的外角性质;注意利用整体思想求出∠CNA与∠MAN的和,而不是求出每一个角的度数是一种很重要的方法,注意掌握.

练习册系列答案
相关题目
19.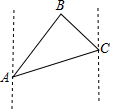 如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45)
如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45)
 如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45)
如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.74,$\sqrt{6}$≈2.45)| A. | 66.8 | B. | 67 | C. | 115.8 | D. | 116 |
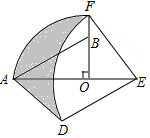 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.
如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是8-π.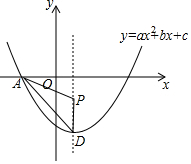 如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)
如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)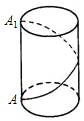 如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?
如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?