题目内容
16.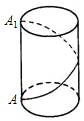 如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?
如图,一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1,若圆柱底面半径为$\frac{6}{π}$,高为5,蚂蚁爬行的最短距离为多少?
分析 先画出圆柱的侧面展开图,然后圆的周长公式可求得AC的长,然后在Rt△ACA′中,依据勾股定理可求得AA′的长.
解答 解:圆柱展开如图所示,则蚂蚁爬行最短距离为AA′.
∵圆柱底面半径为$\frac{6}{π}$,
∴AC=2πR=2π•$\frac{6}{π}$=12.
在Rt△ACA′中,A′C=5,AC=12..
由勾股定理得:AA′=$\sqrt{A′{C}^{2}+A{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
∴蚂蚁最短路程为13cm.
点评 本题主要考查的是平面展开路径最短问题,找出蚂蚁爬行的最短路径是解题的关键.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | x4+x4=2x8 | B. | (-x2)(-x3)=-x5 | C. | (x-y)2(x-y)=(x-y)2 | D. | x3•x=x4 |
6.计算x3•x3=( )
| A. | x5 | B. | x6 | C. | x8 | D. | x9 |
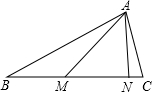 如图,△ABC中,AB=BC,M、N为BC边上的两点,且∠BAM=∠CAN,MN=AN.求∠MAC的度数.
如图,△ABC中,AB=BC,M、N为BC边上的两点,且∠BAM=∠CAN,MN=AN.求∠MAC的度数. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=6,BC=8.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=6,BC=8.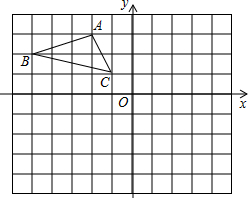 如图,△ABC在第二象限内,顶点A的坐标是(-2,3),
如图,△ABC在第二象限内,顶点A的坐标是(-2,3), 如图所示,网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则S△ABC=6.
如图所示,网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则S△ABC=6.