题目内容
 已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积.
已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积.考点:相似三角形的判定与性质
专题:
分析:由平行可证得△ADE∽△ABC,△CEF∽△CAB,再由条件可分别求出其对应的相似比,可求出△ADE和△CEF的面积,可求得平行四边形BFED的面积.
解答:解:
∵DE∥BC,
∴△ADE∽△ABC,
∵AE:EC=2:3,
∴
=
,
∴
=
,即
=
,
解得S△ADE=
,
同理可得△CEF∽△CAB,
=
,
可求得S△CEF=
,
∴S四边形BFED=S△ABC-S△ADE-S△CEF=
.
∵DE∥BC,
∴△ADE∽△ABC,
∵AE:EC=2:3,
∴
| AE |
| AC |
| 2 |
| 5 |
∴
| S△ADE |
| S△ABC |
| 4 |
| 25 |
| S△ADE |
| 5 |
| 4 |
| 25 |
解得S△ADE=
| 4 |
| 5 |
同理可得△CEF∽△CAB,
| CE |
| CA |
| 3 |
| 5 |
可求得S△CEF=
| 9 |
| 5 |
∴S四边形BFED=S△ABC-S△ADE-S△CEF=
| 12 |
| 5 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
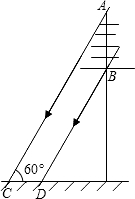 一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )| A、12 | ||||
| B、0.6 | ||||
C、
| ||||
D、
|
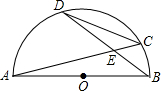 半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=
半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=| 27 |
| 5 |
| A、5 | ||||
| B、4 | ||||
C、3
| ||||
D、
|
若2x2+6x+k2=2(x+
)2,则k等于( )
| 3 |
| 2 |
| A、3 | ||||
| B、-3 | ||||
C、±
| ||||
| D、6个 |
|-2|等于( )
| A、-2 | ||
B、-
| ||
| C、2 | ||
| D、-3与a |
 如图,已知,⊙O的半径为3cm,过直径BA延长线上一点P作直线分别交⊙O于点C,D,若C是PD的中点,且PC=2PA,求PA的长.
如图,已知,⊙O的半径为3cm,过直径BA延长线上一点P作直线分别交⊙O于点C,D,若C是PD的中点,且PC=2PA,求PA的长.



 如图,已知
如图,已知 如图,A、B分别为y=x2上的两点,且AB⊥y轴,若AB=4,则△OAB的面积为
如图,A、B分别为y=x2上的两点,且AB⊥y轴,若AB=4,则△OAB的面积为