题目内容
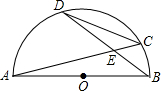 半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=
半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=| 27 |
| 5 |
| A、5 | ||||
| B、4 | ||||
C、3
| ||||
D、
|
考点:圆周角定理,相似三角形的判定与性质
专题:
分析:根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=7-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
解答:解:∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;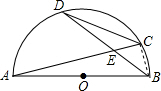
∴
=
=
=
;
设BE=x,则DE=7-x,EC=
x,AE=
(7-x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=x,EC=
x,则BC=
x;
在Rt△ABC中,AC=AE+EC=
-
x,BC=
x;
由勾股定理,得:AB2=AC2+BC2,
即:92=(
-
x)2+(
x)2,
整理,得x2-14x+31=0,
解得:x1=7+3
(不合题意舍去),x2=7-3
;
则DE=7-x=3
.
故选:C.
∴△AEB∽△DEC;

∴
| EC |
| BE |
| DE |
| AE |
| DC |
| AB |
| 3 |
| 5 |
设BE=x,则DE=7-x,EC=
| 3 |
| 5 |
| 5 |
| 3 |
连接BC,则∠ACB=90°;
Rt△BCE中,BE=x,EC=
| 3 |
| 5 |
| 4 |
| 5 |
在Rt△ABC中,AC=AE+EC=
| 35 |
| 3 |
| 16 |
| 15 |
| 4 |
| 5 |
由勾股定理,得:AB2=AC2+BC2,
即:92=(
| 35 |
| 3 |
| 16 |
| 15 |
| 4 |
| 5 |
整理,得x2-14x+31=0,
解得:x1=7+3
| 2 |
| 2 |
则DE=7-x=3
| 2 |
故选:C.
点评:此题主要考查了圆周角定理、相似三角形的判定和性质、勾股定理的应用等知识;本题要特别注意的是BE、DE不是相似三角形的对应边,它们的比不等于相似比,以免造成错解.

练习册系列答案
相关题目
 如图,a、b在数轴上所示,下列判断错误的是( )
如图,a、b在数轴上所示,下列判断错误的是( )| A、a2>b2 |
| B、a-b>0 |
| C、ab<0 |
| D、|b|=-b |
下列图象能表示y是x的函数的图象是( )
A、 |
B、 |
C、 |
D、 |
 已知圆内接正三角形的面积为12
已知圆内接正三角形的面积为12 如图,四条线段AB、BC、CD、DA,用圆规比较图中的线段的大小.
如图,四条线段AB、BC、CD、DA,用圆规比较图中的线段的大小. 已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积.
已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积.