题目内容
 如图,已知
如图,已知| AB |
| DB |
| BC |
| BE |
| CA |
| ED |
考点:相似三角形的判定与性质
专题:
分析:由条件可得△ABC∽△DBE,可得∠ABC=∠DBE,再利用角的和可得到结论.
解答:解:相等,理由如下:
∵
=
=
,
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
即∠ABD+∠DBC=∠DBC+∠CBE,
∴∠ABD=∠CBE.
∵
| AB |
| DB |
| BC |
| BE |
| CA |
| ED |
∴△ABC∽△DBE,
∴∠ABC=∠DBE,
即∠ABD+∠DBC=∠DBC+∠CBE,
∴∠ABD=∠CBE.
点评:本题主要考查相似三角形的判定和性质,掌握两三角形的三边分别对应成比例可判定两三角形相似是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,数轴上A、B上两点分别对应有理数a、b,则下列结论正确的是( )
如图,数轴上A、B上两点分别对应有理数a、b,则下列结论正确的是( )| A、a+b>0 |
| B、ab>0 |
| C、-b>a |
| D、|a|>|b| |
如果一个正多边形的一个内角为120°,则这个正多边形为( )
| A、正五边形 | B、正六边形 |
| C、正七边形 | D、正八边形 |
已知有理数x四舍五入后的近似值是5.4,则x的值不可能是( )
| A、5.35 | B、5.44 |
| C、5.349 | D、5.449 |
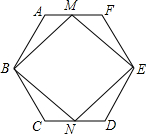 如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为
如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为 在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.
在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF. 如图:在Rt△ABC中,∠ACB=90°,P为AB上一点,Q为BC上一点,且PQ⊥AB,若△BPQ的面积等于四边形APQC的面积的
如图:在Rt△ABC中,∠ACB=90°,P为AB上一点,Q为BC上一点,且PQ⊥AB,若△BPQ的面积等于四边形APQC的面积的 已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积.
已知如图,△ABC中,DE∥BC,若S△ABC=5,AE:EC=2:3,过点E作EF∥AB交BC于F,求平行四边形BFED的面积. 如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若
如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若