题目内容
16.小明在做一道计算题目(2+1)(22+1)(24+1)(28+1)(216+1)的时候是这样分析的:这个算式里面每个括号内都是两数和的形式,跟最近学的两大公式作对比,发现跟平方差公式很类似,但是需要添加两数的差,于是添了(2-1),并做了如下的计算:(2+1)(22+1)(24+1)(28+1)(216+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)
=(22-1)(22+1)(24+1)(28+1)(216+1)
=(24-1)(24+1)(28+1)(216+1)
=(28-1)(28+1)(216+1)
=(216-1)(216+1)
=232-1
请按照小明的方法:
(1)计算(3+1)(32+1)(34+1)(38+1)(316+1)
(2)直接写出(5+1)(52+1)(54+1)…(52016+1)-$\frac{{5}^{4032}}{4}$的值.
分析 根据题意以及平方差公式即可求出答案.
解答 解:(1)原式=$\frac{1}{2}$(3-1)(3+1)(32+1)(34+1)(38+1)(316+1)
=$\frac{1}{2}$(32-1)(32+1)(34+1)(38+1)(316+1)
=$\frac{1}{2}$(34-1)(34+1)(38+1)(316+1)
=$\frac{1}{2}$(38-1)(38+1)(316+1)
=$\frac{1}{2}$(316-1)(316+1)
=$\frac{1}{2}$(332-1)
(2)原式=$\frac{1}{4}$(5-1)(5+1)(52+1)(54+1)…(52016+1)-$\frac{{5}^{4032}}{4}$
=$\frac{1}{4}$(54032-1)-$\frac{{5}^{4032}}{4}$
=-$\frac{1}{4}$
点评 本题考查平方差公式的应用,注意平方差公式的结构.

练习册系列答案
相关题目
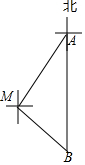 如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处
如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处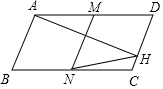 如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=56°.
如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=56°.