题目内容
10.(1)解方程:$\frac{1}{x-1}$-1=$\frac{x}{2x-2}$;(2)解不等式组:$\left\{\begin{array}{l}{\frac{x-1}{2}≤1}\\{x-2<4(x+1)}\end{array}\right.$,并写出该不等式组的正整数解.
分析 (1)先把分式方程变成整式方程,求出方程的解,最后进行检验即可;
(2)先求出不等式的解集,再求出不等式组的解集,最后求出正整数解即可.
解答 解:(1)方程两边都乘以2(x-1)得:2-2(x-1)=x,
解得:x=$\frac{4}{3}$,
检验:当x=$\frac{4}{3}$时,2(x-1)≠0,
所以x=$\frac{4}{3}$是原方程的解,
即原方程的解为x=$\frac{4}{3}$;
(2)解:$\left\{\begin{array}{l}{\frac{x-1}{2}≤1①}\\{x-2<4(x+1)②}\end{array}\right.$
∵解不等式①得:x≤3,
解不等式②得:x>-2,
∴原不等式组的解集为-2<x≤3,
不等式组的正整数解为:1,2,3.
点评 本题考查了解分式方程,解一元一次不等式组,不等式组的整数解的应用,能把分式方程变成整式方程是解(1)小题的关键,能根据不等式的解集求出不等式组的解集是解(2)的关键.

练习册系列答案
相关题目
20.20150=( )
| A. | 0 | B. | 1 | C. | -2015 | D. | 2015 |
18.计算:
(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$.
(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$.
19.下列各式的运算等于a6的是( )
| A. | a2•a3 | B. | a12÷a2 | C. | a3+a3 | D. | (a3)2 |
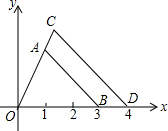 已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).
已知A(1,2),B(3,0),将△AOB以坐标原点O为位似中心扩大到△OCD(如图),D(4,0),则点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).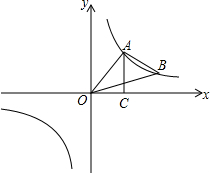 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且点A,B的横坐标分别为a和2a(a>0).过点A作x轴的垂线,垂足为C,连接OA,△AOC的面积为2.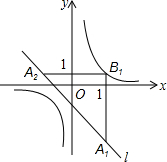 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013=-$\frac{1}{3}$.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线与点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究;过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2013=-$\frac{1}{3}$.