题目内容
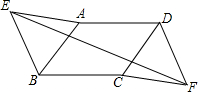 如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:由平行四边形的性质可证△ADE≌△CBF,可得DE=BF,且可得BE=DF,可证明四边形EBFD为平行四边形.
解答: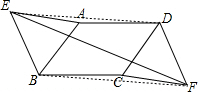 证明:
证明:
如图,连接DE、BF,
∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,∠BAD=∠BCD,
又△BAE、△CDF为等边三角形,
∴AE=BE=AB=CD=CF=DF,∠EAB=∠DCF=60°,
∴∠EAD=∠BCF,
在△ADE和△CBF中
∴△ADE≌△CBF(SAS),
∴DE=BF,
∴四边形EBFD为平行四边形.
 证明:
证明:如图,连接DE、BF,
∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,∠BAD=∠BCD,
又△BAE、△CDF为等边三角形,
∴AE=BE=AB=CD=CF=DF,∠EAB=∠DCF=60°,
∴∠EAD=∠BCF,
在△ADE和△CBF中
|
∴△ADE≌△CBF(SAS),
∴DE=BF,
∴四边形EBFD为平行四边形.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边分别平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目
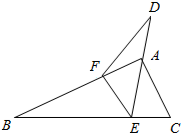 如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )
如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )| A、68° | B、72° |
| C、40° | D、80° |
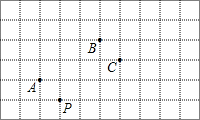 如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )
如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )| A、点A | B、点B | C、点C | D、点P |
 如图所示,关于线段、射线和直线的条数,下列说法正确的是( )
如图所示,关于线段、射线和直线的条数,下列说法正确的是( )| A、五条线段,三条射线 |
| B、一条直线,三条线段 |
| C、三条线段,两条射线,一条直线 |
| D、三条线段,三条射线 |
 如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )
如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )| A、1:2:2:3 |
| B、3:2:2:3 |
| C、1:2:2:1 |
| D、4:2:2:3 |
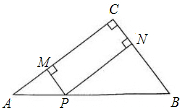 如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.
如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.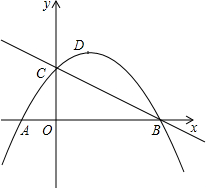 如图,抛物线y=-
如图,抛物线y=-