题目内容
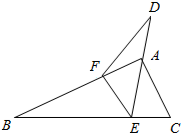 如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )
如图,一纸片△ABC中,AE平分∠BAC,将∠B对折至D,使其边BE的一部分与AE重合,折痕为EF,∠AEC=72°,∠DFA=8°,则∠C的度数为( )| A、68° | B、72° |
| C、40° | D、80° |
考点:翻折变换(折叠问题),三角形内角和定理
专题:
分析:如图,证明∠BAE=∠CAE(设为α);∠B=∠D(设为β);求出α、β的值即可解决问题.
解答: 解:如图,∵AE平分∠BAC,
解:如图,∵AE平分∠BAC,
∴∠BAE=∠CAE(设为α);
由题意得:∠B=∠D(设为β),
∴α=β+8°,∠AEC=α+β=2β+8°,
∵∠AEC=72°,即2β+8°=72°,
∴β=32°,α=40°,
∴∠C=180°-32°-80°=68°,
故选A.
 解:如图,∵AE平分∠BAC,
解:如图,∵AE平分∠BAC,∴∠BAE=∠CAE(设为α);
由题意得:∠B=∠D(设为β),
∴α=β+8°,∠AEC=α+β=2β+8°,
∵∠AEC=72°,即2β+8°=72°,
∴β=32°,α=40°,
∴∠C=180°-32°-80°=68°,
故选A.
点评:该题主要考查了旋转变换的性质、三角形的内角和定理等几何知识点及其应用问题;解题的关键是灵活运用旋转变换的性质、三角形的内角和定理来分析、判断、解答.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
(-1)2n+1+(-1)2n=( )(n为正整数)
| A、2 | B、-2 | C、2或-2 | D、0 |
一个正方形的面积为17,估计它的边长大小为( )
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
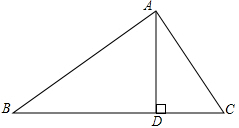 在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.
在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.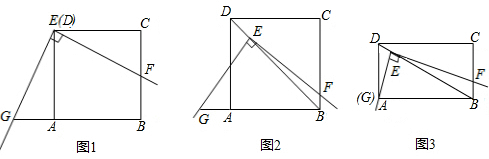
 一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标.
一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标.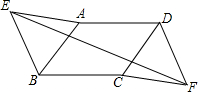 如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.