题目内容
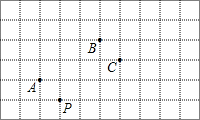如图，在每个小方格都是正方形的网格中，一颗棋子从P点开始依次关于点A，B，C作循环对称跳动，即第一次跳到P点关于A点的对称点M处，第二次跳到M点关于B点的对称点N处，第三次跳到N点关于C点的对称点处，…，以此类推，循环往复，经过2015次跳动后，距离棋子落点最近的点是（ ）| A、点A | B、点B | C、点C | D、点P |
考点：规律型：点的坐标
专题：
分析：首先建立如图所示的坐标系，则P的坐标为（0，-2），连接PA延长到M使MA=PA，所以M的坐标是M（4，4），连接MB延长到N使BN=BM，所以N的坐标是N（-2，0），连接NC延长到P，则PC=NC，所以棋子跳动3次后又回点P处，根据经过第2015次跳动后，棋子落在点N处，即可得出坐标，进而可求出距离棋子落点最近的点．
解答：解：首先建立如图所示的坐标系，则P的坐标为（0，-2），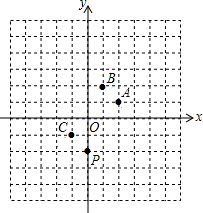
∵棋子跳动3次后又回点P处，
∴经过第2015次跳动后，即2015÷3=671余2，棋子落在点N处，
∴坐标为N（-2，0），
∴距离棋子落点最近的点是C，
故选C．
∵棋子跳动3次后又回点P处，
∴经过第2015次跳动后，即2015÷3=671余2，棋子落在点N处，
∴坐标为N（-2，0），
∴距离棋子落点最近的点是C，
故选C．
点评：本题考查了坐标与图形变化-对称，此类题应首先找到循环的规律，然后进行计算．熟悉：两个点若关于x轴对称，则横坐标不变，纵坐标互为相反数；两个点若关于y轴对称，则横坐标互为相反数，纵坐标不变；两个点若关于原点对称，则横坐标、纵坐标都是互为相反数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
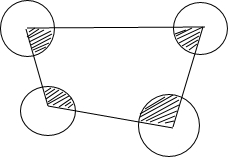如图所示，分别以四边形的各个顶点为圆心，半径为10作圆（这些圆互不相交）．问这些圆与四边形的公共部分（即图中阴影部分）的面积是多少？为什么？
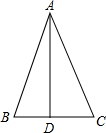如图，在△ABC中，AB=AC，AD是BC边上的高，∠C=63°，BC=4，求∠BAD的度数及DC的长．
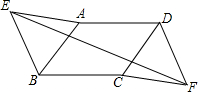如图，在?ABCD中，以AB，DC为边在两侧作等边△AEB和等边△CFD，求证：四边形EBFD是平行四边形．
如图，两个正方形的边上分别为a，b，你能用a，b表示阴影部分的面积吗？若a=12，b=5，则阴影部分的面积是多少？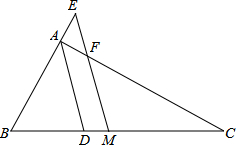
如图，△ABC中∠A的平分线为AD，M为BC的中点，过点M作ME∥AD交BA的延长线于E，交AC于F．
如图，直线y=-