题目内容
已知二次函数y=(k-2)x2+2kx+3k,根据下列给出的条件求出相应的k的值.
(1)抛物线的顶点在x轴上;
(2)抛物线的顶点在y轴上;
(3)抛物线的顶点在y=4x上.
(1)抛物线的顶点在x轴上;
(2)抛物线的顶点在y轴上;
(3)抛物线的顶点在y=4x上.
考点:二次函数的性质
专题:
分析:根据二次函数顶点坐标公式求出顶点,然后根据x轴上点的纵坐标为0,y轴上横坐标为0,一次函数图象上点的坐标特征列出方程求解即可.
解答:解:x=-
=
,
y=
=
,
(1)∵抛物线的顶点在x轴上,
∴
=0,
解得k1=0,k2=3;
(2)∵抛物线的顶点在y轴上,
∴
=0,
解得k=0;
(3)∵抛物线的顶点在y=4x上,
∴4×
=
,
整理得,k2-5k=0,
解得k1=0,k2=5.
| 2k |
| 2(k-2) |
| k |
| k-2 |
y=
| 4(k-2)•3k-(2k)2 |
| 4(k-2) |
| 2k2-6k |
| k-2 |
(1)∵抛物线的顶点在x轴上,
∴
| 2k2-6k |
| k-2 |
解得k1=0,k2=3;
(2)∵抛物线的顶点在y轴上,
∴
| k |
| k-2 |
解得k=0;
(3)∵抛物线的顶点在y=4x上,
∴4×
| k |
| k-2 |
| 2k2-6k |
| k-2 |
整理得,k2-5k=0,
解得k1=0,k2=5.
点评:本题考查了二次函数的性质,坐标轴上点的坐标特征,一次函数图象上点的坐标特征,表示出顶点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列事件是必然事件的是( )
| A、2012年12月31日无锡一定是晴天 |
| B、掷一枚硬币,恰好正面朝上 |
| C、30名同学中至少有两人在同一个月出生 |
| D、打开电视,正在播广告 |
 如图,在△ABC中,DE∥BC,交AB于D,交AC于E,F为BC上的一点,DE交AF于G,AD=2BD,AE=5,求:
如图,在△ABC中,DE∥BC,交AB于D,交AC于E,F为BC上的一点,DE交AF于G,AD=2BD,AE=5,求: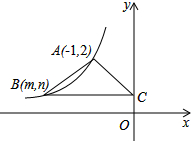 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y= 如图,已知圆内接四边形ABCD中,AB为直径,AD=DC,∠B=40°,则∠A=
如图,已知圆内接四边形ABCD中,AB为直径,AD=DC,∠B=40°,则∠A=