题目内容
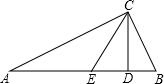 在△ABC中,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,求证:CE=AE=EB.
在△ABC中,∠ACB=90°,CD、CE三等分∠ACB,CD⊥AB,求证:CE=AE=EB.考点:等边三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:通过已知条件可以求得∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,由CD⊥AB,求得∠B=60°,则由直角三角形的两个锐角互余的性质得到∠A=30°,所以∠A=∠ACE,∠B=∠ECB,根据等角对等边即可证得结论;
解答:证明:∵∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,
∵CD⊥AB,
∴∠B=60°,
∴∠A=30°
∴∠A=∠ACE,∠B=∠ECB,
∴AE=EC,EC=EB.
∴CE=AE=EB.
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,
∵CD⊥AB,
∴∠B=60°,
∴∠A=30°
∴∠A=∠ACE,∠B=∠ECB,
∴AE=EC,EC=EB.
∴CE=AE=EB.
点评:本题考查了等腰三角形的判定和性质,等腰三角形的判定和性质,求得∠A=∠ACE,∠B=∠ECB是本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、数轴上的点只能表示整数 |
| B、数轴上的一个点只能表示一个数 |
| C、数轴上的点所表示的数都是有理数 |
| D、两个不同的有理数可以用数轴上同一点表示 |
 小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是
小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是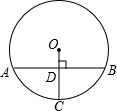 如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是
如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是 如图,AC∥EF∥BD.
如图,AC∥EF∥BD.