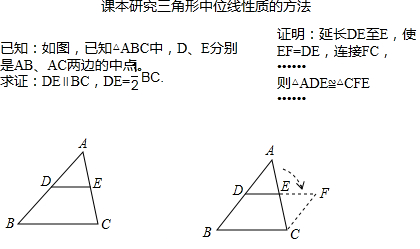
题目内容
4.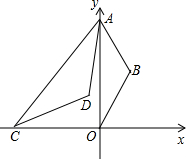 如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.
如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.(1)若点A的纵坐标为6,
①连接BD,求证:△ABD∽△AOC;
②连接OD,求线段OD的最小值.
(2)设点A纵坐标为a,点C的横坐标为c,当△AOD为等腰三角形时,$\frac{c}{a}$的值为$±\sqrt{2}$或$\frac{\sqrt{3}±\sqrt{11}}{4}$.
分析 (1)①由△ABO∽△ADC,推出$\frac{AB}{AD}$=$\frac{AO}{AC}$,推出$\frac{AB}{AO}$=$\frac{AD}{AC}$,由∠CAD=∠OAB,推出∠DAB=∠CAO,即可证明△ABD∽△AOC.
②如图1中,设BD交OA于K.由△ABD∽△AOC,推出∠ABD=∠AOC=90°,推出点D在过点B垂直AB的直线上运动,推出当OD⊥BD时,OD的值最小,解直角三角形即可解决问题.
(2)分四种情形讨论①)①如图2中,当AD=AO时,作DH⊥AC于H.②如图3中,当OA=OD时,作OH⊥BD于H.③如图4中,当OA=OD时,作OH⊥DK于H.④如图5中,当AO=AD时,作DK⊥AC于K.分别构建方程即可解决问题.
解答 解:(1)①如图1中,连接BD、OD.
∵∠ADC=∠ABO=120°,DA=DC,BA=BO.
∴∠DAC=∠DCA=∠BAO=∠BOA=30°,
∴△ABO∽△ADC,
∴$\frac{AB}{AD}$=$\frac{AO}{AC}$,
∴$\frac{AB}{AO}$=$\frac{AD}{AC}$,
∵∠CAD=∠OAB,
∴∠DAB=∠CAO,
∴△ABD∽△AOC.
②如图1中,设BD交OA于K.
∵△ABD∽△AOC,
∴∠ABD=∠AOC=90°,
∴点D在过点B垂直AB的直线上运动,
∴当OD⊥BD时,OD的值最小,
∵∠BAO=∠BOA=30°,∠ABD=90°,
∴∠AKB=60°,∠KBO=∠KOB=30°,
∴KO=KB,设KO=KB=x,则AK=2x,
∵OA=6,
∴3x=6,
∴x=2,
∴OK=2,
在Rt△ODK中,
∵∠DKO=∠AKB=60°,
∴DK=$\frac{1}{2}$OK=1,DO=$\sqrt{3}$DK=$\sqrt{3}$,
∴OD的最小值为$\sqrt{3}$.
(2)①如图2中,当AD=AO时,作DH⊥AC于H.
由题意AD=DC=AO=a,
在Rt△ADH中,AH=AD•cos30°=$\frac{\sqrt{3}}{2}$a,
∴AC=2AH=$\sqrt{3}$a,
在Rt△ACO中,CO=$\sqrt{A{C}^{2}-A{O}^{2}}$=$\sqrt{2}$a,
∴c=-$\sqrt{2}$a,
∴$\frac{c}{a}$=-$\sqrt{2}$.
②如图3中,当OA=OD时,作OH⊥BD于H,
由(1)可知AK=2OK,OK=KB=$\frac{1}{3}$a,AB=$\frac{\sqrt{3}}{3}$a,
在Rt△OHK中,OH=OK•cos30°=$\frac{\sqrt{3}}{6}$a,
在Rt△DHO中,DH=$\sqrt{O{D}^{2}-O{H}^{2}}$=$\sqrt{{a}^{2}-(\frac{\sqrt{3}}{6}a)^{2}}$=$\frac{\sqrt{33}}{6}$a,
∴DB=DH+HK+KB=$\frac{\sqrt{33}}{6}$a+$\frac{1}{2}$a,
∵△ABD∽△AOC,
∴$\frac{AO}{CO}$=$\frac{AB}{BD}$=$\frac{\frac{\sqrt{3}}{3}a}{\frac{\sqrt{33}}{6}a+\frac{1}{2}a}$,
∴$\frac{a}{-c}$=$\frac{\sqrt{11}-\sqrt{3}}{4}$,
∴$\frac{c}{a}$=-$\frac{\sqrt{11}-\sqrt{3}}{4}$=$\frac{\sqrt{3}-\sqrt{11}}{4}$
③如图4中,当OA=OD时,作OH⊥DK于H.
∵由(1)可知AK=2OK,OK=KB=$\frac{1}{3}$a,AB=$\frac{\sqrt{3}}{3}$a,
在Rt△OHK中,OH=OK•cos30°=$\frac{\sqrt{3}}{6}$a,
在Rt△ODH中,DH=$\sqrt{O{D}^{2}-O{H}^{2}}$=$\frac{\sqrt{33}}{6}$a,
∴BD=DH-KH-KB=$\frac{\sqrt{33}}{6}$a-$\frac{1}{2}$a,
∵△ABD∽△AOC,
∴$\frac{AO}{CO}$=$\frac{AB}{BD}$=$\frac{\frac{\sqrt{3}}{3}a}{\frac{\sqrt{33}}{6}a-\frac{1}{2}a}$=$\frac{\sqrt{11}+\sqrt{3}}{4}$,
∴$\frac{a}{c}$=$\frac{\sqrt{11}+\sqrt{3}}{4}$,
④如图5中,当AO=AD时,作DK⊥AC于K.
在Rt△ADK中,AK=AD•cos30°=$\frac{\sqrt{3}}{2}$a,
∴AC=$\sqrt{3}$a,
在Rt△AOC中,OC=$\sqrt{A{C}^{2}-A{O}^{2}}$=$\sqrt{2}$a,
∴c=$\sqrt{2}$a,
∴$\frac{c}{a}$=$\sqrt{2}$,
综上所述,当△ADO是等腰三角形时,$\frac{c}{a}$的值为$±\sqrt{2}$或$\frac{\sqrt{3}±\sqrt{11}}{4}$.
故答案为$±\sqrt{2}$或$\frac{\sqrt{3}±\sqrt{11}}{4}$.
点评 本题考查相似综合题、等腰三角形的性质、勾股定理、30度角的直角三角形的性质、相似三角形的判定和性质垂线段最短等知识,解题的关键是学会应用垂线段最短解决最短问题,学会用分类讨论的思想思考问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | (-1)2017 | B. | (-3)0 | C. | $\sqrt{9}$ | D. | ($\frac{1}{2}$)-2 |
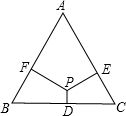 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )| A. | 6cm | B. | 7cm | C. | 10cm | D. | 12cm |
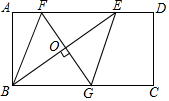 如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.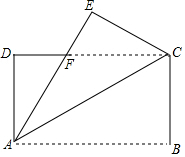 如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.
如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.