题目内容
9．
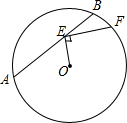如图，已知⊙O的半径为5，弦AB=8，点E在AB上运动，连结OE，过点E作EF⊥OE交⊙O于点F，当EF最大时，OE+EF的值为7．
分析 当OE⊥AB，EF最大，即点F与点B重合，过O作OE⊥AB于E，连接OB，根据垂径定理得到BE=4，根据勾股定理得到OE=$\sqrt{O{B}^{2}-B{E}^{2}}$=3，于是得到结论．
解答 
解：当OE⊥AB，EF最大，即点F与点B重合，
过O作OE⊥AB于E，连接OB，
∵AB=8，
∴BE=4，
∵OB=5，
∴OE=$\sqrt{O{B}^{2}-B{E}^{2}}$=3，
∴OE+EF=OE+OB=7，
故答案为：7．
点评 本题考查了垂径定理，勾股定理，正确的作出辅助线是解题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，A、P、B、C是⊙O上的四个点，∠APC=∠CPB=60°．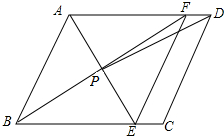
如图，在?ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD，若AB=4，AD=6，∠ABC=60°，PD的长2$\sqrt{7}$，四边形ABEF的面积8$\sqrt{3}$．
如图，点D、E分别是等边三角形ABC的两边AB、AC上的点，且∠BOD=60°，求证：AD=CE．
如图，△ABC≌△AED，BC⊥DE，则∠D的度数为45°．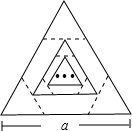
边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点顺次连接，又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图）…，按此方式依次操作，则第7个正六边形的边长是$\frac{1}{3}$×（$\frac{1}{2}$）6a．