题目内容
【题目】已知，AB是⊙O的直径，AB＝8，点C在⊙O的半径OA上运动，PC⊥AB，垂足为C，PC＝5，PT为⊙O的切线，切点为T．
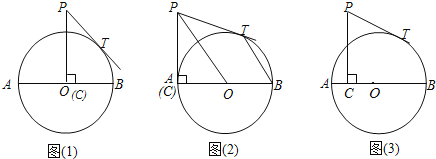
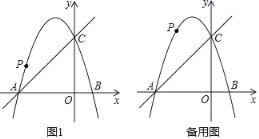
（1）如图1，当C点运动到O点时，求PT的长；
（2）如图2，当C点运动到A点时，连接PO、BT，求证：PO∥BT；
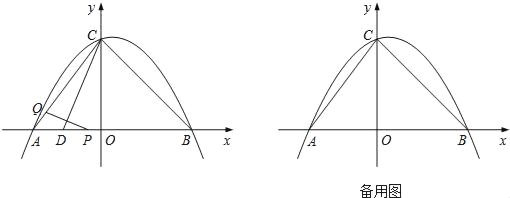
（3）如图3，设PT＝y，AC＝x，求y与x的解析式并求出y的最小值．
【答案】（1）PT＝3；（2）见解析；（3）y＝
，y最小＝3．
【解析】
（1）连接OT，根据题意，由勾股定理可得出PT的长；
（2）连接OT，则OP平分劣弧AT，则∠AOP＝∠B，从而证出结论；
（3）设PC交⊙O于点D，延长线交⊙O于点E，由相交弦定理，可得出CD的长，再由切割线定理可得出y与x之间的关系式，进而求得y的最小值．
解：如图（1），连接OT，
∵PC＝5，OT＝4，
∴由勾股定理得，
（2）证明：如图（2）连接OT，
∵PT，PC为⊙O的切线，
∴∠OPA＝∠OPT，∠PAO＝∠PTO，
∴∠POA＝∠POT，
∵∠AOT＝2∠B，
∴∠AOP＝∠B，
∴PO∥BT；
（3）解：如图（3），连接PO，PT
∵AB是⊙O的直径，AB＝8，AC＝x
∴CO＝4﹣x；
又∵PC⊥AB
∴
∴y＝
∴
．
练习册系列答案
相关题目
【题目】已知y＝|y1|+y2﹣1，其中y1＝x﹣3，y2与x成反比例关系，且当x＝2时，y2＝3．
（1）根据给定的条件写出y与x的函数表达式及自变量x的取值范围： ．
（2）当x＞0时，根据y与x的函数表达式，选取适当的自变量x的值，完成下表，并根据表中数据，在平面直角坐标系xOy中描点，画出该函数x＞0时的图象．
x | …… | …… | |||||||
y | …… | …… |
（3）当x＞0时，结合函数图象，解决相关问题：估计y＝﹣
x+5时，x的值约为 ．（保留一位小数）
