Question

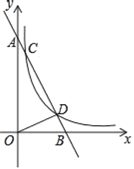
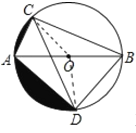
【题目】如图，AB为⊙O的直径，弦，，的平分线交⊙O于点D，求：

（1）BC，AD的长；

（2）图中两阴影部分面积之和．

Answer 1

【答案】(1), ；(2) ．

【解析】

（1）根据直径得出∠ACB＝∠ADB＝90，根据勾股定理求出BC，根据圆周角定理求出AD＝BD，求出AD即可；

（2）根据三角形的面积公式，求出△AOC和△AOD的面积，再求出S扇形COD，即可求出答案．

（1）∵AB是直径，

∴∠ACB＝∠ADB＝90（直径所对的圆周角是直角），

在Rt△ABC中，∠ABC＝30，AC＝4，

∴AB＝8，

∴BC＝=4，

∵∠ACB的平分线交⊙O于点D，

∴∠DCA＝∠BCD

∴，

∴AD＝BD，

∴在Rt△ABD中，AD＝BD＝AB＝4；

（2）连接OC，OD，

∵∠ABC＝30，

∴∠AOC＝2∠ABC＝60，

∵OA＝OB=4，

∴S△AOC＝S△ABC＝××AC×BC＝××4×4＝4，

由（1）得∠AOD＝90，

∴∠COD＝150，

S△AOD＝×AO×OD＝×42＝8，

∴S阴影＝S扇形CODS△AOCS△AOD＝4-8＝．