题目内容
20.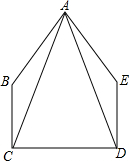 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
分析 (1)根据∠ACD=∠ADC,∠BCD=∠EDC=90°,可得∠ACB=∠ADE,进而运用SAS即可判定全等三角形;
(2)根据全等三角形对应角相等,运用五边形内角和,即可得到∠BAE的度数.
解答 (1)证明:
∵AC=AD,
∴∠ACD=∠ADC,
又∵∠BCD=∠EDC=90°,
∴∠ACB=∠ADE,
在△ABC和△AED中,
$\left\{\begin{array}{l}{BC=ED}\\{∠ACB=∠ADE}\\{AC=AD}\end{array}\right.$,
∴△ABC≌△AED(SAS);
(2)解:当∠B=140°时,∠E=140°,
又∵∠BCD=∠EDC=90°,
∴五边形ABCDE中,∠BAE=540°-140°×2-90°×2=80°.
点评 本题主要考查了全等三角形的判定与性质的运用,解题时注意:两边及其夹角对应相等的两个三角形全等.

练习册系列答案
相关题目
10.为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
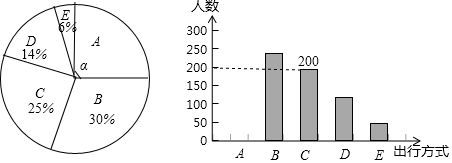
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有800人,其中选择B类的人数有240人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
| 种类 | A | B | C | D | E |
| 出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有800人,其中选择B类的人数有240人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
5.在平面直角坐标系中,点 P(1,2)关于原点的对称点 P'的坐标是( )
| A. | (1,2) | B. | (-1,2) | C. | (1,-2) | D. | (-1,-2) |
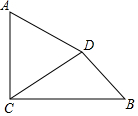 如图,已知AC⊥BC,垂足为C,AC=4,BC=3$\sqrt{3}$,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
如图,已知AC⊥BC,垂足为C,AC=4,BC=3$\sqrt{3}$,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.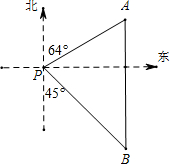 如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).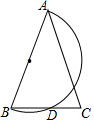 如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则$\widehat{{A}D}$的度数是140度.
如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则$\widehat{{A}D}$的度数是140度.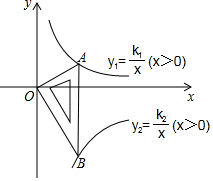 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.
如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.