题目内容
12.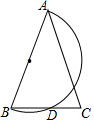 如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则$\widehat{{A}D}$的度数是140度.
如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则$\widehat{{A}D}$的度数是140度.
分析 首先连接AD,由等腰△ABC中,AB=AC,以AB为直径的半圆交BC于点D,可得∠BAD=∠CAD=20°,即可得∠ABD=70°,继而求得∠AOD的度数,则可求得$\widehat{AD}$的度数.
解答  解:连接AD、OD,
解:连接AD、OD,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=20°,BD=DC,
∴∠ABD=70°,
∴∠AOD=140°
∴$\widehat{AD}$的度数为140°;
故答案为140.
点评 此题考查了圆周角定理以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.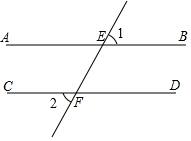 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠1=60°,则∠2等于( )| A. | 120° | B. | 30° | C. | 40° | D. | 60° |
7.数据-2,-1,0,1,2,4的中位数是( )
| A. | 0 | B. | 0.5 | C. | 1 | D. | 2 |
17.25的算术平方根是( )
| A. | 5 | B. | ±5 | C. | -5 | D. | 25 |
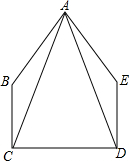 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD. 2016年,我国又有1240万人告别贫困,为世界脱贫工作作出了卓越贡献.将1240万用科学记数法表示为a×10n的形式,则a的值为1.24.
2016年,我国又有1240万人告别贫困,为世界脱贫工作作出了卓越贡献.将1240万用科学记数法表示为a×10n的形式,则a的值为1.24.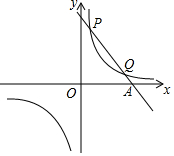 已知一次函数y=k1x+b与反比例函数y=$\frac{k_2}{x}$的图象交于第一象限内的P($\frac{1}{2}$,8),Q(4,m)两点,与x轴交于A点.
已知一次函数y=k1x+b与反比例函数y=$\frac{k_2}{x}$的图象交于第一象限内的P($\frac{1}{2}$,8),Q(4,m)两点,与x轴交于A点.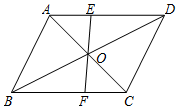 如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )