题目内容
4.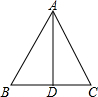 如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )
如图,在△ABC中,∠B=∠C,AD为△ABC的中线,那么下列结论错误的是( )| A. | △ABD≌△ACD | B. | AD为△ABC的高线 | ||
| C. | AD为△ABC的角平分线 | D. | △ABC是等边三角形 |
分析 据等角对等边得出AC=AB,根据等腰三角形性质推出AD⊥BC,AD为△ABC的角平分线,根据AAS可以证出△ABD≌△ACD,根据以上结论推出即可.
解答 解:∵∠B=∠C,
∴AB=AC,
∵AD是△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD,即AD是△ABC的高,AD为△ABC的角平分线,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中
$\left\{\begin{array}{l}{∠B=∠C}\\{∠ADC=∠ADB}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD,
即选项A、B、C都正确,
根据已知只能推出AC=AB,不能推出AC、AB和BC的关系,
即不能得出△ABC是等边三角形,选项D错误,
故选D.
点评 本题考查了全等三角形的性质,等腰三角形的性质和判定,等边三角形的判定,熟记等腰三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 相等的角是对顶角 | |
| C. | 三角形的外角等于两个内角的和 | |
| D. | 若三条直线两两相交,则共有6对对顶角 |
13.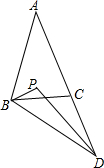 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )| A. | 105° | B. | 110° | C. | 130° | D. | 145° |
14. 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |

 如图,已知AB∥CD,∠A=60°,∠C=20°,则∠E=40°.
如图,已知AB∥CD,∠A=60°,∠C=20°,则∠E=40°.