题目内容
关于x的整系数一元二次方程ax2-bx+c=0(a≠0)中,若a+b是偶数,c是奇数,则( )
| A、方程没有整数根 |
| B、方程有两个相等的整数根 |
| C、方程有两个不相等的整数根 |
| D、不能判定方程整数根的情况 |
考点:一元二次方程的整数根与有理根
专题:
分析:假设出方程解的情况,当有奇数时与有偶数时,分别讨论即可求出.
解答:解:∵a+b是偶数,c是奇数,
∴a、b是偶数,c是奇数,或者a、b、c都是奇数;
①a、b是偶数,c是奇数.
当方程有奇数解时,方程x(ax+b)-c=0,
左边=奇×(偶×奇+偶)-奇=奇≠0=右边;
当方程有偶数解时,方程x(ax+b)-c=0,
左边=偶×(偶×偶+偶)+奇=奇≠0=右边.
∴方程没有整数解.
②a、b、c都是奇数.
当方程有奇数解时,方程x(ax+b)-c=0,
左边=奇×(奇×奇+奇)-奇=奇≠0=右边;
当方程有偶数解时,方程x(ax+b)-c=0,
左边=偶×(奇×偶+奇)-奇=奇≠0=右边.
∴方程没有整数解.
综上所述,方程没有整数根;
故选:A.
∴a、b是偶数,c是奇数,或者a、b、c都是奇数;
①a、b是偶数,c是奇数.
当方程有奇数解时,方程x(ax+b)-c=0,
左边=奇×(偶×奇+偶)-奇=奇≠0=右边;
当方程有偶数解时,方程x(ax+b)-c=0,
左边=偶×(偶×偶+偶)+奇=奇≠0=右边.
∴方程没有整数解.
②a、b、c都是奇数.
当方程有奇数解时,方程x(ax+b)-c=0,
左边=奇×(奇×奇+奇)-奇=奇≠0=右边;
当方程有偶数解时,方程x(ax+b)-c=0,
左边=偶×(奇×偶+奇)-奇=奇≠0=右边.
∴方程没有整数解.
综上所述,方程没有整数根;
故选:A.
点评:此题主要考查了一元二次方程根整数根的有关知识,以及整数的奇偶性,难度不大,题目比较典型.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,在⊙O中,直径AB垂直弦CD,E为BC弧上一点,下列结论:
如图,在⊙O中,直径AB垂直弦CD,E为BC弧上一点,下列结论:①∠1=∠2;②∠3=2∠4;③∠3+∠5=180°.
其中正确的是( )
| A、①③ | B、①② | C、①②③ | D、②③ |
 如图所示,其中∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
如图所示,其中∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )| A、180° | B、225° |
| C、360° | D、120° |
已知实数a,b(其中a>0)满足a+
=4,b2+b=4,则
+
的值是( )
| a |
| 1 |
| a |
| 1 |
| b2 |
A、
| ||||||
B、
| ||||||
C、±
| ||||||
D、
|
下列图形中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
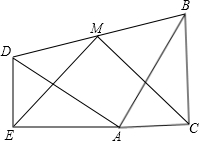 如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.
如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.