题目内容
等腰三角形两边长为2,5,P为底边上任一点,P到两腰距离之和是 .
考点:勾股定理,三角形的面积,等腰三角形的性质
专题:
分析:连接AD,根据等腰三角形的性质可表示出S△ABC=S△ABD+S△ACD的值,再根据S△ABC=
AB•CG,即可得到ED+FD=CG;然后利用三角形的面积求得CG的值.
| 1 |
| 2 |
解答: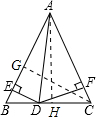 解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.
解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.
∵2+2<5,
∴等腰△ABC的腰AB=AC=5;
∴AH=
=2
;
有∵AB=AC,
∴S△ABC=S△ABD+S△ACD=
AB•ED+
AC•FD=
AB•(ED+FD),
∴ED+FD=CG;
∵S△ABC=
AB•CG=
BC•AH,
∴CG=
,即ED+FD=
;
故答案是:
.
 解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.
解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.∵2+2<5,
∴等腰△ABC的腰AB=AC=5;
∴AH=
| 52-12 |
| 6 |
有∵AB=AC,
∴S△ABC=S△ABD+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ED+FD=CG;
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CG=
4
| ||
| 5 |
4
| ||
| 5 |
故答案是:
4
| ||
| 5 |
点评:本题综合考查了勾股定理、三角形的面积、等腰三角形的面积.解答此题的关键是求得ED+FD=CG.

练习册系列答案
相关题目
 如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
关于x的整系数一元二次方程ax2-bx+c=0(a≠0)中,若a+b是偶数,c是奇数,则( )
| A、方程没有整数根 |
| B、方程有两个相等的整数根 |
| C、方程有两个不相等的整数根 |
| D、不能判定方程整数根的情况 |
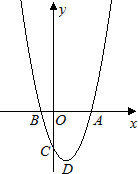 已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.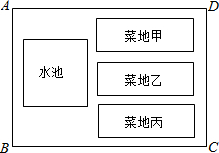 如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.
如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长. 如图,已知两组对应边互相垂直的两角之差为45°,则这两个角的度数为
如图,已知两组对应边互相垂直的两角之差为45°,则这两个角的度数为