题目内容
先化简,再求值:-3(2x3-xy2+5y)-3(-5+xy2+x3-2y),其中x=1,y=-1.
考点:整式的加减—化简求值
专题:
分析:首先提取公因式(-3),然后合并同类项,再运用乘法分配原则进行乘法运算,最后代入值计算即可.
解答:解:原式=-3(2x3-xy2+5y-5+xy2+x3-2y)
=-3(3x3+3y-5)
=-9x3-9y+15.
当x=1,y=-1时,
原式=-9×1+9×1+15
=15.
=-3(3x3+3y-5)
=-9x3-9y+15.
当x=1,y=-1时,
原式=-9×1+9×1+15
=15.
点评:本题主要考查提取公因式,合并同类项,乘法分配原则等知识点,关键在于正确的运用相关的运算法则对原式进行化简,认真的进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x2+ax+b=0的两根为x1,x2,且x13+x23=x12+x22=x1+x2,则有序实数组(a,b)共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
关于x的整系数一元二次方程ax2-bx+c=0(a≠0)中,若a+b是偶数,c是奇数,则( )
| A、方程没有整数根 |
| B、方程有两个相等的整数根 |
| C、方程有两个不相等的整数根 |
| D、不能判定方程整数根的情况 |
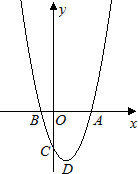 已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.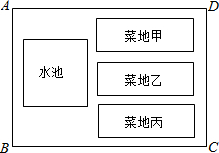 如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.
如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.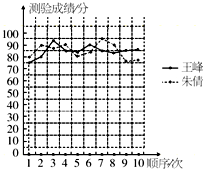 光华中学要选派一名学生去参加区级电脑知识竞赛,王峰和朱倩两位同学平时电脑都学的不错,为了确定谁去参赛,老师对他们的电脑知识进行了10次模拟测验,测验成绩情况如下面的折线统计图(如图):
光华中学要选派一名学生去参加区级电脑知识竞赛,王峰和朱倩两位同学平时电脑都学的不错,为了确定谁去参赛,老师对他们的电脑知识进行了10次模拟测验,测验成绩情况如下面的折线统计图(如图):