题目内容
5.观察分析下列方程:①x+$\frac{2}{x}$=3;②x+$\frac{6}{x}$=5;③x+$\frac{12}{x}$=7,请利用他们所蕴含的规律,写出这一组方程中的第n个方程是x+$\frac{n(n+1)}{x}$=n+(n+1).分析 方程中的分式的分子变化规律为:n(n+1),方程的右边的变化规律为n+(n+1).
解答 解:∵第1个方程为x+$\frac{1×2}{x}$=1+2,
第2个方程为x+$\frac{2×3}{x}$=2+3,
第3个方程为x+$\frac{3×4}{x}$=3+4,
…
∴第n个方程为x+$\frac{n(n+1)}{x}$=n+(n+1).
故答案是:x+$\frac{n(n+1)}{x}$=n+(n+1).
点评 本题考查了分式的定义.该题属于寻找规律的题目,对于此类题型,应观察哪部分没有发生变化,哪部分发生了变化,变化的规律是什么.

练习册系列答案
相关题目
15.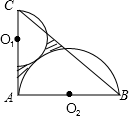 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
 如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为6的等腰直角三角形,直角边AB是半圆O2的直径,半圆O1过C点且与半圆O2相切,则图中阴影部分的面积是( )| A. | $\frac{46-13π}{4}$ | B. | $\frac{32-9π}{2}$ | C. | $\frac{23-13π}{4}$ | D. | $\frac{54-13π}{4}$ |
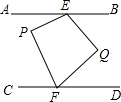 已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.
已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.