题目内容
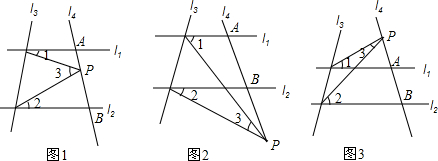
3.已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上.的一个定点如图1)(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上.的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
分析 (1)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(2)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(3)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(4)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可.
解答 解:
(1)延长DP交直线l2于E,如图1,
∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠3=∠DEC+∠2,
∴∠3=∠2+∠1;
(2)不变化,∠3=∠1+∠2,
理由是:∵直线 l1∥l2,
∴∠DEC=∠1,
∴∠3=∠2+∠DEC=∠1+∠2,
(3)①当点P在射线AB上运动时,如图2,
∵直线 l1∥l2,
∴∠PFB=∠1,
∴∠PFB=∠2+∠3,
∴∠1=∠2+∠3,
②如图3,当点P在射线BA上运动时,
∵直线 l1∥l2,
∴∠PGA=∠2,
∴∠PGA=∠1+∠3,
∴∠2=∠1+∠3.
点评 本题考查了平行线性质的应用,主要考查学生的推理能力,用了运动观点.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
15.若不等式ax-2>0的解集为x<-2,则关于y的方程ay+2=0的解是( )
| A. | y=-1 | B. | y=-2 | C. | y=1 | D. | y=2 |
13.1纳米=0.000 000 001米,则2.5纳米应表示为( )米.
| A. | 2.5×10-8 | B. | 2.5×10-9 | C. | 2.5×10-10 | D. | 2.5×109 |
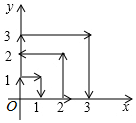 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第28秒时跳蚤所在位置的坐标是(3,5).
一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第28秒时跳蚤所在位置的坐标是(3,5).

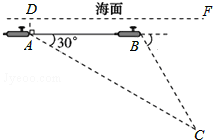 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.
如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为55°.