题目内容
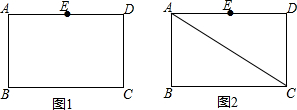
2.已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点C处,使三角板绕点C旋转.(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明;
(2)在(1)的条件下,若BE:CE:DE=1:2:3,求∠BEC的度数;
(3)若BC=2,点M是边AB的中点,连结CM,CM与BD交于点O,当三角板的一边CF与边CM重合时(如图2),若OF=$\frac{\sqrt{5}}{6}$,求DN的长.
分析 (1)证DE与BF所在的三角形全等即可;
(2)设BE=k,由BE:CE:DE=1:2:3,可得到BE、EF,根据勾股定理逆定理可知∠BEF=90°,进而求出∠BEC的度数;
(3)根据△CFN∽△CDO,进而得到△BOM∽△DOC,利用相似三角形的性质解答.
解答 解:(1)如图1,当三角板旋转到图1的位置时,DE=BF,
∵∠ECB+∠BCF=90°,∠DCE+∠ECB=90°,
∴∠DCE=∠BCF.
∵∠BCD=90°,AB∥CD
∴∠ABC=90°,∠BAC=∠ACD,
∵BC=2,AB=1,
∴tan∠BAC=2,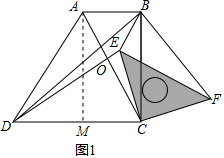
∵tan∠ADC=2,
∴∠BAC=∠ADC,
∴∠ACD=∠ADC,
∴AD=AC,
作AM⊥CD于点M,
∴CD=2MC=2AB=2,
∴CD=BC.
∵EC=CF,
∴△DCE≌△BCF.
∴DE=BF.
(2)设BE=k,
∵BE:CE:DE=1:2:3,
∴BF=3k,EF=2$\sqrt{2}$k,
∵k2+(2$\sqrt{2}$k)2=(3k)2,
∴∠BEF=90°,
∴∠BEC=∠BEF+∠CEF=90°+45°=135°;
(3)∵∠CEF=∠CDO=45°,∠FCN=∠DCO,
∴△CFN∽△CDO,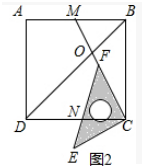
∴$\frac{CF}{CD}=\frac{CN}{CO}$,
∵点M是边AB的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$BC=1,
∵AB∥CD,
∴∠MBF=∠ODC,∠BMF=∠OCD,
∴△BOM∽△DOC,
∴$\frac{OM}{OC}=\frac{OB}{OD}=\frac{MB}{DC}=\frac{1}{2}$,
在Rt△CBM中,
CM=$\sqrt{B{C}^{2}+B{M}^{2}}$=$\sqrt{5}$,
∴CO=$\frac{2\sqrt{5}}{3}$,
∵OF=$\frac{\sqrt{5}}{6}$,
∴CF=$\frac{\sqrt{5}}{2}$,
∴$\frac{CN}{\frac{2\sqrt{5}}{3}}=\frac{\sqrt{5}}{2}$,
∴CN=$\frac{5}{6}$,
∴DN=2-$\frac{5}{6}$=$\frac{7}{6}$.
点评 本题是一道几何变换综合题,主要考查了图形旋转的性质、等腰直角三角形的性质、矩形的性质、全等三角形的判定与性质、勾股定理及逆定理、相似三角形的判定与性质等知识的综合运用,综合性很强,难度适中,第3小题是本题难点,发现相似三角形转移线段比进行计算是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | -3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
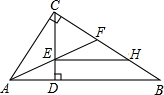 在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.
在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.