题目内容
7.已知方程ax2+bx+9=0有一个根为x1=-12,且关于x的方程ax2+bx+9=$\frac{3}{4}$x+$\frac{21}{4}$有两个相等的实数根,求a、b的值.分析 先根据根据一元二次方程的解的定义得到144a-12b+9=0,再根据根的判别式得到(b-$\frac{3}{4}$)2-4a(9-$\frac{21}{4}$)=0然后解方程组得到a=$\frac{5}{48}$,b=2.
解答 解:∵方程ax2+bx+9=0有一个根为x1=-12,关于x的方程ax2+bx+9=$\frac{3}{4}$x+$\frac{21}{4}$有两个相等的实数根,
∴144a-12b+9=0,(b-$\frac{3}{4}$)2-4a(9-$\frac{21}{4}$)=0,
解$\left\{\begin{array}{l}{144a-12b+9=0}\\{(b-\frac{3}{4})^{2}-4a(9-\frac{21}{4})=0}\end{array}\right.$,
得:a=$\frac{5}{48}$,b=2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解.

练习册系列答案
相关题目
15.把x2y-2y2x+y3分解因式正确的是( )
| A. | y(x+y)(x-y) | B. | y(x-y)2 | C. | y(x2-2xy+y2) | D. | (x-2y)2 |
2.连续四次抛掷一枚硬币都是正面朝上,则“第五次抛掷正面朝上”是( )
| A. | 必然事件 | B. | 不可能事件 | C. | 随机事件 | D. | 概率为1的事件 |
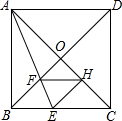 如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )
如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )