题目内容
20.从甲、乙、丙、丁4名学生中随机抽取2名学生担任数学小组长,则抽取到甲和乙概率为$\frac{1}{6}$.分析 根据题意画出树状图,然后求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:画树形图得:
∵一共有12种情况,抽取到甲和乙的有2种,
∴P(抽到甲和乙)=$\frac{2}{12}$=$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
10.已知函数y=(1-2k)x是正比例函数,且y随x的增大而减小,那么k的取值范围是( )
| A. | k<$\frac{1}{2}$ | B. | k>$\frac{1}{2}$ | C. | k>0 | D. | k<1 |
8.数轴上表示整数的点称为整点.某数轴上的单位长度是1cm,若在这个数轴上随意画出一条长2016cm的线段AB,则线段AB盖住的整点个数是( )
| A. | 2017个或2018个 | B. | 2016个或2017个 | C. | 2015个或2016个 | D. | 2014个或2015个 |
5.函数y=-$\frac{1}{4}$(2x-1)2+1的二次项系数为( )
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
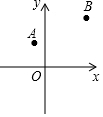 如图,在平面直角坐标系中,点A(-2,1),B(6,2),点P是x轴上一动点.求:
如图,在平面直角坐标系中,点A(-2,1),B(6,2),点P是x轴上一动点.求: 如图所示的图案由六个全等的直角三角形组成,点O是该图案的中心,则该图案可看成由一个直角三角形绕O点顺时针依次旋转60得到,或可看成由两个相邻的直角三角形绕O点顺时针依次旋转120°得到,或可看成由三个相邻的直角三角形绕O点旋转180°得到.
如图所示的图案由六个全等的直角三角形组成,点O是该图案的中心,则该图案可看成由一个直角三角形绕O点顺时针依次旋转60得到,或可看成由两个相邻的直角三角形绕O点顺时针依次旋转120°得到,或可看成由三个相邻的直角三角形绕O点旋转180°得到.