题目内容
17.我们知道,平方数的开平方运算可以直接求得,如$\sqrt{4}$等,有些数则不能直接求得,如$\sqrt{5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:| a | … | 0.04 | 4 | 400 | 40000 | … |
| $\sqrt{a}$ | … | x | 2 | y | z | … |
(2)用公式表示这一规律:当a=4×100n(n为整数)时,$\sqrt{a}$=2×10n;
(3)利用这一规律,解决下面的问题:
已知$\sqrt{5.56}$≈2.358,则①$\sqrt{0.0556}$≈0.2358;②$\sqrt{556}$≈23.58.
分析 (1)利用算术平方根定义计算,填表即可;
(2)归纳总结得到一般性规律,求出$\sqrt{a}$的值即可;
(3)利用得出的规律计算即可得到结果.
解答 解:(1)根据题意得:x=0.2;y=20;z=200;
(2)当a=4×100n(n为整数)时,$\sqrt{a}$=2×10n;
(3)若$\sqrt{5.56}$≈2.358,则①$\sqrt{0.0556}$≈0.2358;②$\sqrt{556}$≈23.58.
故答案为:(1)0.2;20;200;(2)2×10n;(3)0.2358;23.58.
点评 此题考查了算术平方根,熟练掌握算术平方根的定义是解本题的关键.

练习册系列答案
相关题目
7. 已知实数a、b在数轴上表示的点如图,化简|a+b|的结果为( )
已知实数a、b在数轴上表示的点如图,化简|a+b|的结果为( )
 已知实数a、b在数轴上表示的点如图,化简|a+b|的结果为( )
已知实数a、b在数轴上表示的点如图,化简|a+b|的结果为( )| A. | a+b | B. | -a-b | C. | 0 | D. | 2a |
3.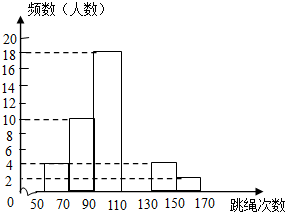 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
(1)a=10,b14.
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:| 组别 | 次数x | 频数(人数) |
| 第1组 | 50≤x<70 | 2 |
| 第2组 | 70≤x<90 | a |
| 第3组 | 90≤x<110 | 18 |
| 第4组 | 110≤x<130 | b |
| 第5组 | 130≤x<150 | 4 |
| 第6组 | 150≤x<170 | 2 |
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
 如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
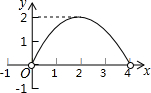
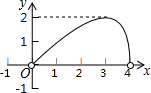
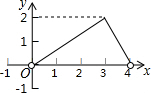
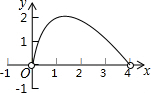
如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.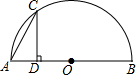 如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )