题目内容
8. 如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF和等腰Rt△ABE,∠FOB=∠ABE=90°,连结EF交y轴于P点.设BP=y,OB=x,请写出y关于x的函数表达式y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
分析 作EN⊥y轴于N,根据余角的性质得到∠NBE=∠BAO,推出△ABO≌△BEN(AAS),根据全等三角形的性质得到NE=OB=x,BN=AO=6,由△OBF是等腰直角三角形,得到BF=$\sqrt{2}$x,推出△OFP∽△PHE,根据相似三角形的性质得到$\frac{OP}{PN}=\frac{OF}{NE}$=1,得到OP=$\frac{1}{2}$ON=$\frac{1}{2}$(6+x即可得到结论.
解答 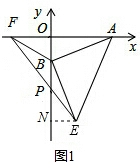 解:如图1,作EN⊥y轴于N,
解:如图1,作EN⊥y轴于N,
∵∠ENB=∠BOA=∠ABE=90°,
∴∠OBA+∠NBE=90°,∠OBA+∠OAB=90°,
∴∠NBE=∠BAO,
在△ABO和△BEN中,$\left\{\begin{array}{l}{∠AOB=∠BNE}\\{∠BAO=∠NBE}\\{AB=BE}\end{array}\right.$,
,∴△ABO≌△BEN(AAS),
∴NE=OB=x,BN=AO=6,
∵△OBF是等腰直角三角形,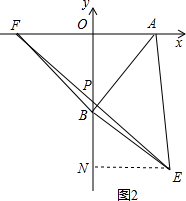
∴BF=$\sqrt{2}$x,
∵∠FOP=∠ENP=90°,∠OPF=∠NPE,
∴△OFP∽△PHE,
∴$\frac{OP}{PN}=\frac{OF}{NE}$=1,
∴OP=$\frac{1}{2}$ON=$\frac{1}{2}$(6+x),
∴BP=OP-OB=3+$\frac{1}{2}$x-x=3-$\frac{1}{2}$x=y,(0<x<6),
当x=6时,y=0,∴F,E,B共线,
当x>6时,如图2,同理得到:OP=$\frac{1}{2}$PN=$\frac{1}{2}$(6+x),PB=OB-OP=x-$\frac{1}{2}$(6+x)=$\frac{1}{2}$x-3=y.
∴y关于x的函数表达式为:y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
故答案为:y=$\left\{\begin{array}{l}{3-\frac{1}{2}x(0<x<6)}\\{0(x=6)}\\{\frac{1}{2}x-3(x>6)}\end{array}\right.$.
点评 本题考查了三角形内角和定理,全等三角形的性质和判定,坐标与图形性质等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.

| A. | 20000(1+x)2=80000 | B. | 20000(1+x)+20000(1+x)2=80000 | ||
| C. | 20000(1+x2)=80000 | D. | 20000+20000(1+x)+20000(1+x)2=80000 |
| a | … | 0.04 | 4 | 400 | 40000 | … |
| $\sqrt{a}$ | … | x | 2 | y | z | … |
(2)用公式表示这一规律:当a=4×100n(n为整数)时,$\sqrt{a}$=2×10n;
(3)利用这一规律,解决下面的问题:
已知$\sqrt{5.56}$≈2.358,则①$\sqrt{0.0556}$≈0.2358;②$\sqrt{556}$≈23.58.
 如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→B→C→M路径匀速慢跑,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )
如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→B→C→M路径匀速慢跑,那么李老师离出发点M的距离y与时间x之间的函数关系的大致图象是( )



 (1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;
(1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;