题目内容
5.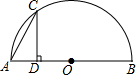 如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )| A. | 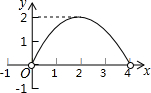 | B. | 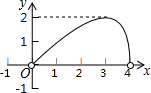 | ||
| C. | 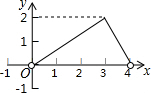 | D. | 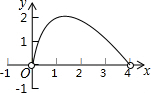 |
分析 连结BC,如图,根据圆周角定理得到∠ACB=90°,则利用勾股定理得到BC=$\sqrt{16-{x}^{2}}$,再利用面积法可得到y=$\frac{x•\sqrt{16-{x}^{2}}}{4}$,CD为半径时最大,即y的最大值为2,此时x=2$\sqrt{2}$,由于y与x函数关系的图象不是抛物线,也不是一次函数图象,则可判断A、C错误;利用y最大时,x=2$\sqrt{2}$可对B、D进行判断.
解答 解:连结BC,如图,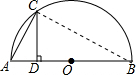
∵AB为直径,
∴∠ACB=90°,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{16-{x}^{2}}$,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴y=$\frac{x•\sqrt{16-{x}^{2}}}{4}$,
∵y的最大值为2,此时x=2$\sqrt{2}$.
故选B.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是利用圆周角定理得到∠ACB=90°.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
20.华为手机营销按批量投入市场,第一次投放20000台,第三次投放80000台,每次按相同的增长率投放,设增长率为x,则可列方程( )
| A. | 20000(1+x)2=80000 | B. | 20000(1+x)+20000(1+x)2=80000 | ||
| C. | 20000(1+x2)=80000 | D. | 20000+20000(1+x)+20000(1+x)2=80000 |
10.已知等腰三角形的一边为2,一边为5,那么它的周长等于( )
| A. | 9 | B. | 12 | C. | 9或12 | D. | 7或10 |
17.我们知道,平方数的开平方运算可以直接求得,如$\sqrt{4}$等,有些数则不能直接求得,如$\sqrt{5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:
(1)表格中的三个值分别为:x=0.2;y=20;z=200;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,$\sqrt{a}$=2×10n;
(3)利用这一规律,解决下面的问题:
已知$\sqrt{5.56}$≈2.358,则①$\sqrt{0.0556}$≈0.2358;②$\sqrt{556}$≈23.58.
| a | … | 0.04 | 4 | 400 | 40000 | … |
| $\sqrt{a}$ | … | x | 2 | y | z | … |
(2)用公式表示这一规律:当a=4×100n(n为整数)时,$\sqrt{a}$=2×10n;
(3)利用这一规律,解决下面的问题:
已知$\sqrt{5.56}$≈2.358,则①$\sqrt{0.0556}$≈0.2358;②$\sqrt{556}$≈23.58.
 (1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;
(1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;