题目内容
9. 如图所示,⊙O的半径是5,它的弦AB=8,OC⊥AB交AB于点D,则CD=2.
如图所示,⊙O的半径是5,它的弦AB=8,OC⊥AB交AB于点D,则CD=2.
分析 连接OA,先根据垂径定理求出AD的长,再由勾股定理求出OD的长,进而可得出结论.
解答  解:连接OA,
解:连接OA,
∵AB=8,OC⊥AB,OA=5,
∴AD=$\frac{1}{2}$AB=4,
∴OD=$\sqrt{{OA}^{2}-{AD}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴CD=OC-OD=5-3=2.
故答案为:2.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
19. 如图,AB∥CD,BE交CD于点D,∠B=34°,∠DEC=90°,则∠C的度数为( )
如图,AB∥CD,BE交CD于点D,∠B=34°,∠DEC=90°,则∠C的度数为( )
 如图,AB∥CD,BE交CD于点D,∠B=34°,∠DEC=90°,则∠C的度数为( )
如图,AB∥CD,BE交CD于点D,∠B=34°,∠DEC=90°,则∠C的度数为( )| A. | 17° | B. | 34° | C. | 56° | D. | 124° |
17. 如图,已知直线AB、CD相交于点O,∠D=105°,如果DE∥AB,那么∠AOC的度数是( )
如图,已知直线AB、CD相交于点O,∠D=105°,如果DE∥AB,那么∠AOC的度数是( )
 如图,已知直线AB、CD相交于点O,∠D=105°,如果DE∥AB,那么∠AOC的度数是( )
如图,已知直线AB、CD相交于点O,∠D=105°,如果DE∥AB,那么∠AOC的度数是( )| A. | 75° | B. | 85° | C. | 95° | D. | 105° |
4.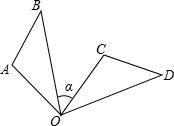 如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
 如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
14. 如图,∠ACB=90°,AD∥EF,∠1=24°,则∠A的度数为( )
如图,∠ACB=90°,AD∥EF,∠1=24°,则∠A的度数为( )
 如图,∠ACB=90°,AD∥EF,∠1=24°,则∠A的度数为( )
如图,∠ACB=90°,AD∥EF,∠1=24°,则∠A的度数为( )| A. | 66° | B. | 67° | C. | 60° | D. | 45° |