题目内容
4．
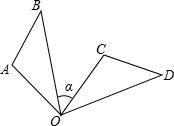如图，△OAB绕点O顺时针旋转85°到△OCD，已知∠A=110°，若∠D=40°，则∠α的度数是（ ）| A． | 30° | B． | 45° | C． | 55° | D． | 60° |
分析 先根据旋转的性质得∠C=∠A=110°，∠BOD=85°，则利用三角形内角和计算出∠COD=30°，然后利用∠BOC=∠BOD-∠COD进行计算即可．
解答 解：∵△OAB绕点O顺时针旋转85°到△OCD，
∴∠C=∠A=110°，∠BOD=85°，
∵∠COD+∠C+∠D=180°，
∴∠COD=180°-110°-40°=30°，
∴∠BOC=∠BOD-∠COD=85°-30°=55°，
即∠α的度数是55°．
故选C．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
15．下列各组图形中，哪一组是全等三角形（ ）
| A． | 都有一锐角为60°的两个直角三角形 | |
| B． | 腰对应相等的两个等腰三角形 | |
| C． | 边长都为5的两个等边三角形 | |
| D． | 面积相等的两个等腰三角形 |
19．
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=$\frac{{m}^{2}+2m-9}{x}$的图象上，若点A的坐标为（-2，3），则m的值为（ ）
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=$\frac{{m}^{2}+2m-9}{x}$的图象上，若点A的坐标为（-2，3），则m的值为（ ）| A． | 1 | B． | 3 | C． | 3或-5 | D． | 1或-3 |
如图所示，⊙O的半径是5，它的弦AB=8，OC⊥AB交AB于点D，则CD=2．
13．以$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$为解的二元一次方程组是（ ）
| A． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ |