题目内容
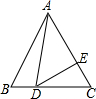 如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=
如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:如图,证明AB=5,∠B=∠C=60°;证明△ABD∽△DCE,得到
=
,求出CE即可解决问题.
| AB |
| CD |
| BD |
| CE |
解答: 解:如图,∵△ABC为等边三角形,
解:如图,∵△ABC为等边三角形,
∴AB=BC=2+3=5,∠B=∠C=60°;
∵∠ADE=60°,
∴∠BAD+∠ADB=∠ADB+∠EDC,
∴∠BAD=∠EDC,而∠B=∠C,
∴△ABD∽△DCE,
∴
=
,
解得:CE=
.
故答案为
.
 解:如图,∵△ABC为等边三角形,
解:如图,∵△ABC为等边三角形,∴AB=BC=2+3=5,∠B=∠C=60°;
∵∠ADE=60°,
∴∠BAD+∠ADB=∠ADB+∠EDC,
∴∠BAD=∠EDC,而∠B=∠C,
∴△ABD∽△DCE,
∴
| AB |
| CD |
| BD |
| CE |
解得:CE=
| 6 |
| 5 |
故答案为
| 6 |
| 5 |
点评:该题以等边三角形为载体,主要考查了等边三角形的性质、相似三角形的判定及其性质的应用等问题;牢固掌握定理是灵活运用、解题的关键.

练习册系列答案
相关题目
在一次“爱心互助”捐款活动中,某班第一小组8名同学捐款的金额(单位:元)如表所示:这8名同学捐款的平均金额约为( )
| 金额/元 | 5 | 6 | 7 | 10 |
| 人数 | 2 | 3 | 2 | 1 |
| A、6.5元 | B、6元 |
| C、3.5元 | D、7元 |
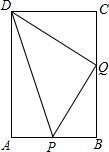 如图,在长方形ABCD中,AB=6cm,BC=12cm,点p 从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,且当点P到达点B时,两点同时停止运动.问几秒时△PBQ的面积等于7cm2?
如图,在长方形ABCD中,AB=6cm,BC=12cm,点p 从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,且当点P到达点B时,两点同时停止运动.问几秒时△PBQ的面积等于7cm2? 如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB. 如图,灌溉渠的横截面是等腰梯形,底宽为2米,坡角为45°,水深为x米,横截面有水的面积为y平方米,y是x的函数,则函数图象是( )
如图,灌溉渠的横截面是等腰梯形,底宽为2米,坡角为45°,水深为x米,横截面有水的面积为y平方米,y是x的函数,则函数图象是( )


 如图,四边形ABCD是周长为40的菱形,点A的坐标是(0,8),则点B的坐标为
如图,四边形ABCD是周长为40的菱形,点A的坐标是(0,8),则点B的坐标为
 如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=
如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=