题目内容
20.已知函数y=(2m+1)x+m-3,若这个函数的图象不经过第二象限,则m的取值范围是( )| A. | m>-$\frac{1}{2}$ | B. | m<3 | C. | -$\frac{1}{2}$<m<3 | D. | -$\frac{1}{2}$<m≤3 |
分析 根据一次函数的图象不经过第二象限列出关于m的不等式组,求出m的取值范围即可.
解答 解:∵一次函数y=(2m+1)x+m-3,的图象不经过第二象限,
∴$\left\{\begin{array}{l}{2m+1>0}\\{m-3≤0}\end{array}\right.$,
解得:-$\frac{1}{2}$<m≤3.
故选D.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时,函数的图象经过一三四象限是解答此题的关键.

练习册系列答案
相关题目
15.一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
| A. | 3 | B. | 2.9 | C. | 2.8 | D. | 2.7 |
12.若不等式组$\left\{\begin{array}{l}{x<2m+1}\\{x>7-m}\end{array}\right.$无解,则m的取值范围是( )
| A. | m=2 | B. | m<2 | C. | m≤2 | D. | m≥2 |
9.长方形的周长为60cm,其中一条边为x(其中x>0),面积为ycm2,则在这个长方形中,y与x的关系可以写为( )
| A. | y=60x-2x2 | B. | y=30x-x2 | C. | y=$\frac{1}{2}$x2-60 | D. | y=$\frac{1}{2}$x2-30 |
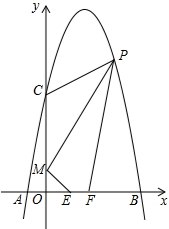 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.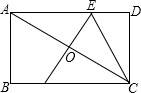 在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.
在矩形ABCD中,已知AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,求CE的长.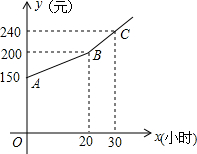 为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.
为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.