题目内容
11.(1)解方程组$\left\{\begin{array}{l}{x=1-y①}\\{3x+y=1②}\end{array}\right.$(2)计算:$\sqrt{4}$-$\root{3}{8}$+|$\sqrt{2}$-$\sqrt{3}$|
分析 (1)方程组利用代入消元法求出解即可;
(2)原式利用算术平方根,立方根,以及绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)将①代入②得:3-3y+y=1,即y=1,
把y=1代入①得:x=0,
则方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$;
(2)原式=2-2+$\sqrt{3}$-$\sqrt{2}$=$\sqrt{3}$-$\sqrt{2}$.
点评 此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.若方程组$\left\{\begin{array}{l}{2kx+(k-1)y=3}\\{3x+4y=1}\end{array}\right.$的解x和y互为相反数,则k的值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
16.下列图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 菱形 | B. | 平行四边形 | C. | 等边三角形 | D. | 梯形 |
3.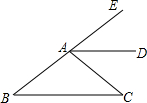 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 80° |
20.已知函数y=(2m+1)x+m-3,若这个函数的图象不经过第二象限,则m的取值范围是( )
| A. | m>-$\frac{1}{2}$ | B. | m<3 | C. | -$\frac{1}{2}$<m<3 | D. | -$\frac{1}{2}$<m≤3 |
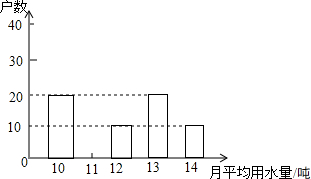 市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.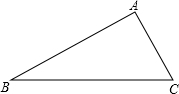 如图,已知三角形ABC,AB=8,BC=10,AC=6,问:
如图,已知三角形ABC,AB=8,BC=10,AC=6,问: